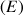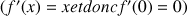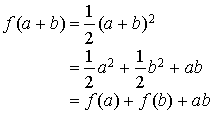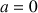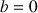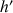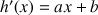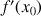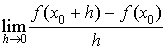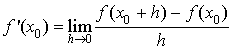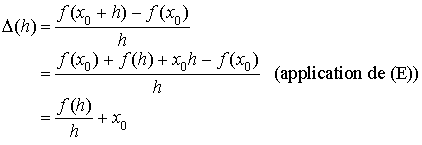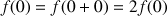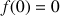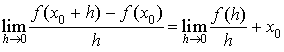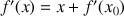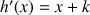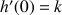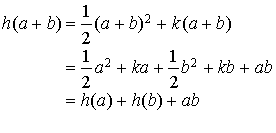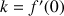Résolution d'une équation fonctionnelle
Introduction
Durée : 50 minutes
Niveau : difficile
Résolution d'une équation fonctionnelle
Le but de cet exercice est de trouver l'ensemble des fonctions solutions d'une équation fonctionnelle.
On note
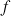les fonctions définies sur R, dérivables en 0 et qui vérifient, quels que soient les réels
et
,
.
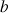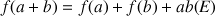1) Existence d'une fonction solution
Vérifier que la fonction
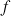définie sur R par 
est une solution.
2) Recherche des fonctions
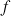solutions
a.
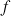désignant une fonction solution, pour
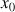réel, soit
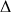la fonction définie sur R* par 
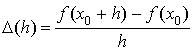; démontrer que 
.
b.
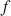désignant une fonction solution, justifier que
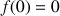puis en déduire que pour tout réel
,
.
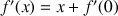c. En déduire que si
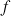est une fonction solution, alors pour tout 
, 
.
3) Réciproquement, vérifier que toute fonction
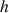définie par 
avec
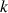constante réelle est une solution.
