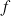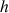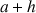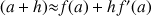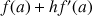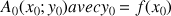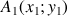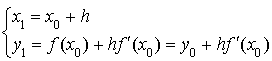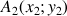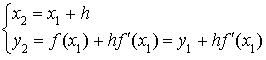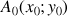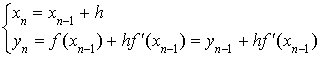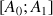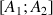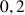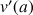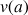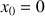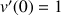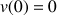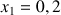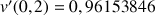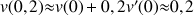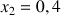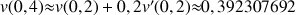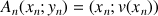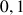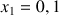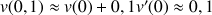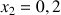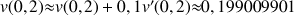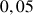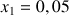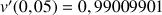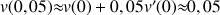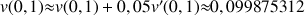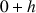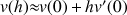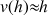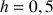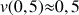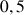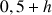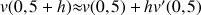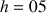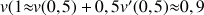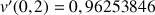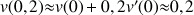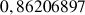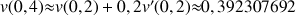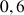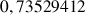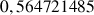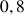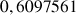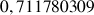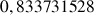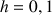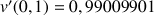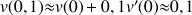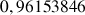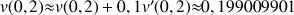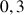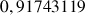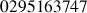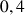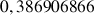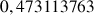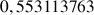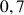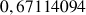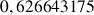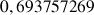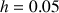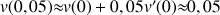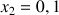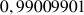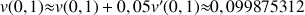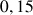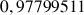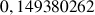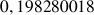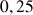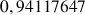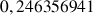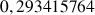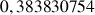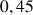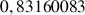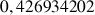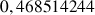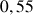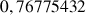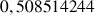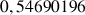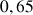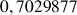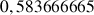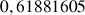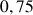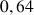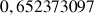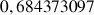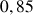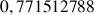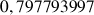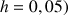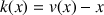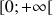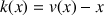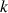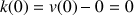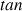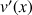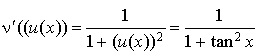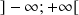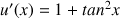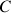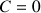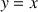Vers une nouvelle fonction : la fonction arctangente
Introduction
Durée : 90 minutes
Niveau : difficile
Vers une nouvelle fonction : la fonction arctangente
1) Soit v une fonction dérivable sur R telle que :
et 
a. Ecrire l'approximation affine locale de la fonction
en 0.
b. En déduire une valeur approchée de
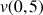et de
.
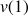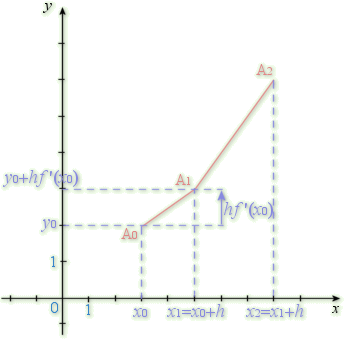
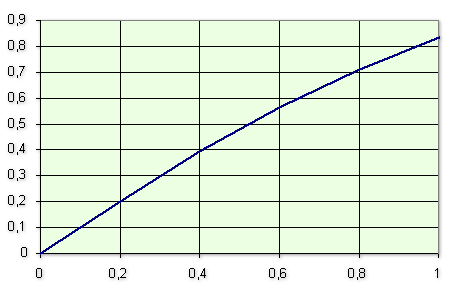
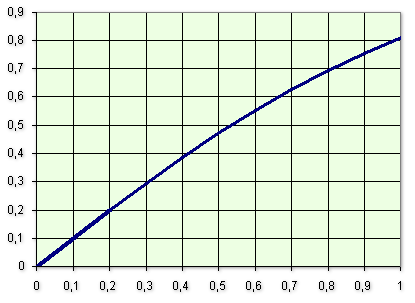
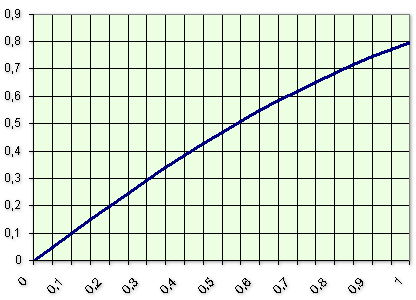
c. Appliquer la méthode d'Euler pour construire à la main une représentation graphique de la fonction
sur
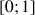en prenant un pas égal à 0,2.
d. Appliquer la même méthode en utilisant une calculatrice ou un tableur avec un pas de 0,1 puis de 0,05.
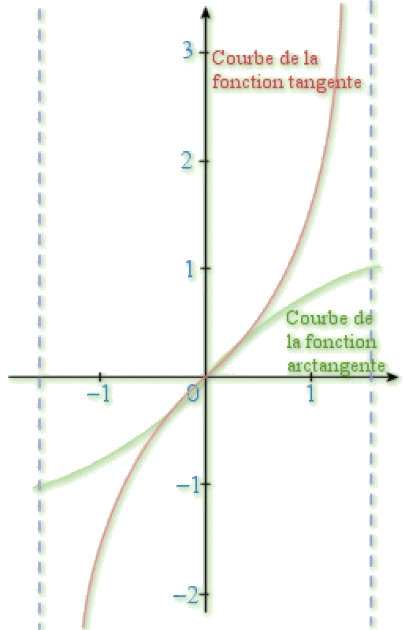
e. Donner une valeur approchée de
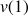. Comparer ce résultat à
.
2) En utilisant le sens de variations de deux fonctions, démontrer que pour tout
de
, 
.
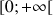3) a.Soit
la fonction tangente.
Démontrer que : pour tout
de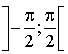 
, on a 
.
b. Déterminer 
.
c. Déduire des questions précédentes que, pour tout
de 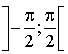, on a 
.
