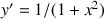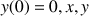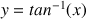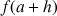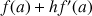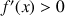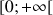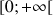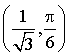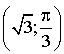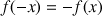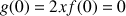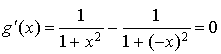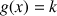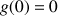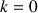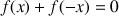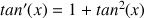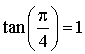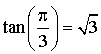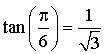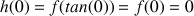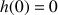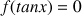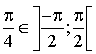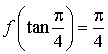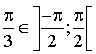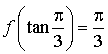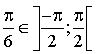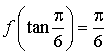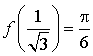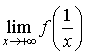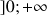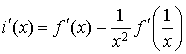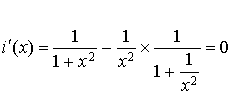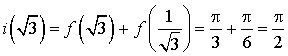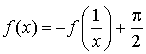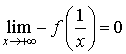Résolution d'une équation différentielle
Introduction
Durée : 90 minutes
Niveau : très difficile
Résolution d'une équation différentielle
On note
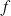les fonctions dérivables sur R qui vérifient, pour tout 
, 
.
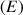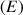est appelée une équation différentielle. On admet qu'il n'existe qu'une seule fonction
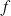solution de
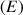vérifiant
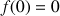; le but de l'exercice est de trouver des propriétés de
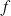qui permettent d'établir son tableau de variation et l'allure de sa courbe.
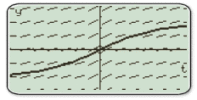
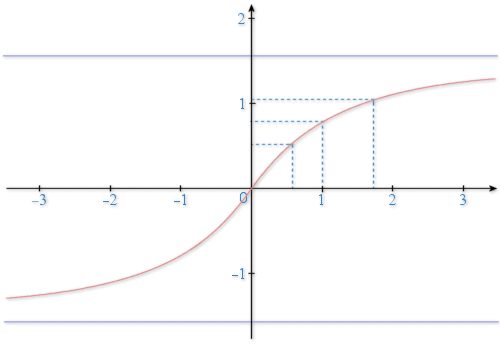
1) Observer, à l'aide d'une machine à calculer, le champ des tangentes des fonctions solutions, et la représentation graphique approchée de la solution vérifiant
.
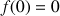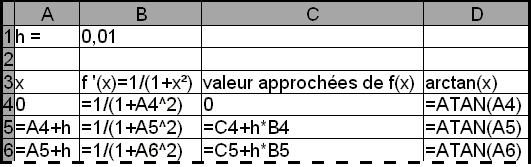
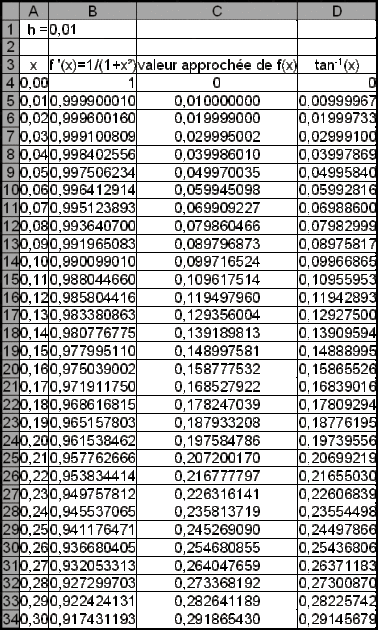
2) A l'aide d'un tableur et de la méthode d'Euler,
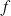étant la solution de
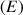vérifiant
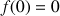, observer des valeurs approchées de
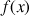pour
, 
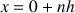, le pas
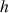étant égal à 0,01.
Comparer avec les valeurs approchées de tan-1 (x) (sur les tableurs, cette fonction se note généralement ATAN).
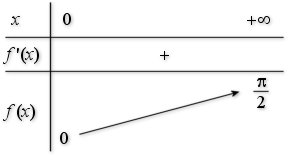
3) Etablir le tableau de variations de
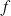pour
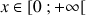; en déduire l'allure de la représentation graphique de
.
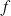Résolution d'une équation différentielle (2)
Soit
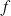la fonction vérifiant : pour tout , et
.
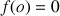1) Etude de la parité de
:
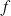On note
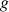la fonction définie sur R par
.
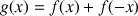Calculer
.
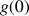Justifier que pour tout ,
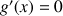puis en déduire que
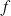est impaire.
2) Recherche des images
, 
, 
:
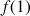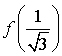On note
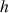la fonction définie sur 
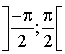par
.
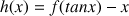Calculer h(0).
Justifier que pour tout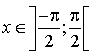 
,
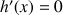et que
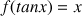; en déduire les valeurs de
, , .
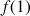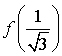3) Etude de la limite en
:
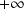Soit
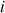la fonction définie sur
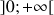par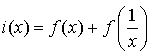 
.
Justifier que pour tout
, 
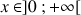et que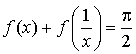 
.
En déduire que 
.
