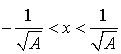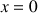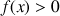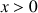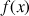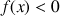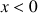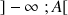Conjecturer: limite d'une fonction en un point
Soit
définie pour 
par : 
.
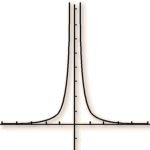
1) Conjecturer, à partir de la courbe représentative de
donnée par une calculatrice, la limite de
en 0.
2) Pour quelles valeurs de
a-t-on
?
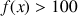3) Soit
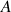un réel strictement positif.
Justifier que
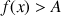lorsque
est assez proche de 0.
Que peut-on en déduire pour la courbe représentative de
?
Soit
définie pour par : 
.
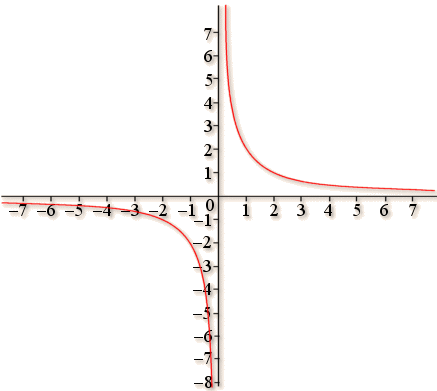
1) Tracer la courbe représentative de
.
2) Justifier que pour tout réel
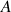, il existe un réel
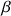tel que : si
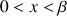alors
.
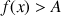On écrira alors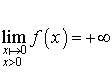 
.
3) Justifier que pour tout réel
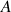, il existe un réel
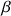tel que : si
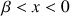alors
.
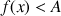On écrira alors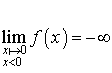 
.
