Limites en l'infini
Définition : Limite l en +∞
Dire qu'une fonction
 , définie sur
, définie sur
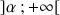 , tend vers le réel
, tend vers le réel
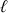 quand
quand
 tend vers
tend vers
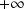 signifie que quel que soit l'intervalle ouvert
signifie que quel que soit l'intervalle ouvert
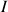 contenant
contenant
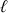 , cet intervalle
, cet intervalle
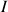 contient toutes les valeurs
contient toutes les valeurs
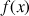 pour
pour
 assez grand.
assez grand.
On écrira : ![]() ou
ou ![]() .
.
On dit alors que la droite d'équation
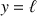 est asymptote à la courbe
est asymptote à la courbe
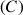 de
de
 au voisinage de
au voisinage de
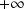 .
.
Exemple :

Exemple :

Définition : Limite l en - ∞
Dire qu'une fonction
 , définie sur
, définie sur
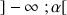 , tend vers le réel
, tend vers le réel
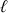 quand
quand
 tend vers
tend vers
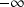 signifie que quel que soit l'intervalle ouvert
signifie que quel que soit l'intervalle ouvert
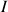 contenant
contenant
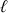 , cet intervalle
, cet intervalle
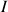 contient toutes les valeurs
contient toutes les valeurs
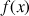 pour
pour
 négatif et assez grand en valeur absolue.
négatif et assez grand en valeur absolue.
On écrira : ![]() ou
ou ![]() .
.
On dit alors que la droite d'équation
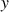 =
=
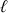 est asymptote à la courbe
est asymptote à la courbe
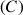 de
de
 au voisinage de
au voisinage de
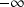 .
.
Exemple :

Définition : Fonction tendant vers +∞ en +∞
Dire qu'une fonction
 , définie sur
, définie sur
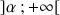 , tend vers
, tend vers
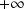 quand
quand
 tend vers
tend vers
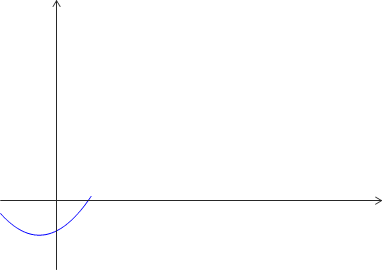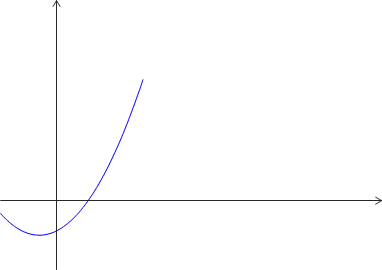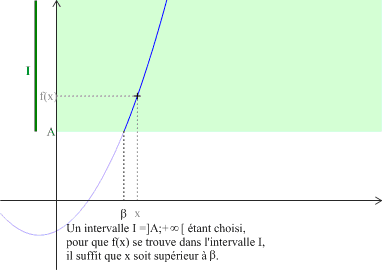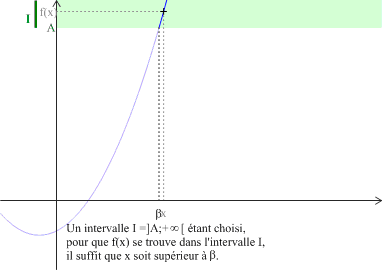
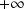 signifie que tout intervalle
signifie que tout intervalle
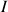 du type
du type
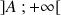 contient toutes les valeurs
contient toutes les valeurs
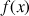 pour
pour
 assez grand.
assez grand.
On écrira : ![]() ou
ou ![]() .
.
Exemple :
Définition : Fonction tendant vers +∞ en -∞
Dire qu'une fonction
 , définie sur
, définie sur
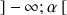 , tend vers
, tend vers
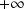 quand
quand
 tend vers
tend vers
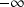 signifie que tout intervalle
signifie que tout intervalle
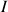 du type
du type
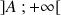 contient toutes les valeurs
contient toutes les valeurs
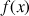 pour
pour
 négatif et assez grand en valeur absolue.
négatif et assez grand en valeur absolue.
On écrira : ![]() ou
ou ![]() .
.
Définition : Fonction tendant vers -∞ en +∞
Dire qu'une fonction
 , définie sur
, définie sur
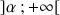 , tend vers
, tend vers
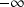 quand
quand
 tend vers
tend vers
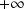 signifie que tout intervalle
signifie que tout intervalle
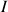 du type
du type
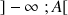 contient toutes les valeurs
contient toutes les valeurs
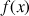 pour
pour
 assez grand.
assez grand.
On écrira : ![]() ou
ou ![]() .
.
Définition : Fonction tendant vers -∞ en -∞
Dire qu'une fonction
 , définie sur
, définie sur
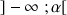 , tend vers
, tend vers
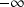 quand
quand
 tend vers
tend vers
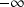 signifie que tout intervalle
signifie que tout intervalle
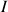 du type
du type
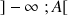 contient toutes les valeurs
contient toutes les valeurs
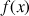 pour
pour
 négatif et assez grand en valeur absolue.
négatif et assez grand en valeur absolue.
On écrira : ![]() ou
ou ![]() .
.






