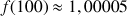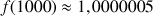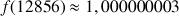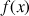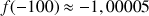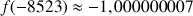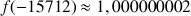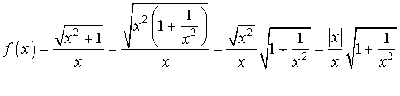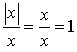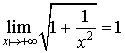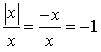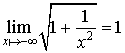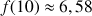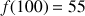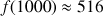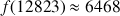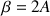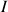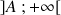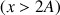Conjecturer: les limites d'une fonction en l'infini
On considère la fonction
définie pour
différent de 0 par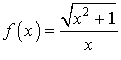 
.
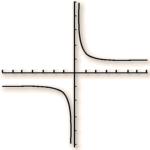
1) Conjecturer, à partir de la courbe représentative de
donnée par une calculatrice, la limite de
en
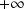et la limite de
en
.
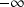2) Donner des valeurs approchées de :
;
;
;
;
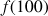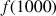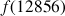
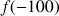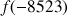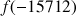
Ces valeurs sont-elles conformes à la conjecture faite ?
3) Justifier que pour
différent de 0,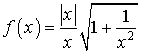 
.
Que peut-on en déduire pour les limites de
en
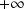et en
?
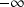On considère la fonction
définie pour 
par :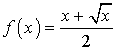 
.
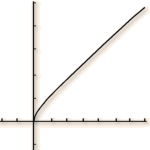
1) Conjecturer, à partir de la courbe représentative de
donnée par une calculatrice, la limite de
en
.
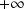2) Donner des valeurs approchées de :
(10) ;
(100) ;
(1000) ;
(12823).
Ces valeurs sont-elles conformes à la conjecture faite ?
3) Justifier que pour tout
, 
.
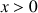En déduire que pour tout réel
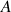, il existe un réel
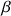tel que : si
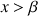alors
.
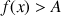Que peut-on en déduire ?
