1) Les transformations du plan
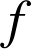 et
et
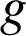 ont pour écriture complexe respectivement
ont pour écriture complexe respectivement ![]() et
et ![]() .
.
Après avoir justifié que
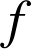 et
et
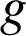 sont des similitudes dont vous préciserez le rapport, déterminer l'écriture complexe des composées
sont des similitudes dont vous préciserez le rapport, déterminer l'écriture complexe des composées ![]() et
et ![]() .
.
L'écriture complexe de
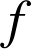 est de la forme
est de la forme ![]() avec
avec ![]() c'est donc une similitude de rapport
c'est donc une similitude de rapport ![]() .
.
L'écriture complexe de
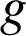 est de la forme
est de la forme ![]() avec
avec ![]() , c'est donc une similitude de rapport
, c'est donc une similitude de rapport ![]() .
.
L'écriture complexe de ![]() est
est ![]() .
.
L'écriture complexe de ![]() est
est ![]() .
.
Les écritures complexes de ![]() et
et ![]() permettent de retrouver que la composée de 2 similitudes de rapport
permettent de retrouver que la composée de 2 similitudes de rapport
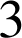 et
et
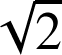 est une similitude de rapport
est une similitude de rapport
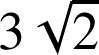
![]() et que
et que ![]() .
.
2)
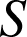 est la réflexion d'axe
est la réflexion d'axe ![]() axe des abscisses du repère
axe des abscisses du repère ![]() du plan et
du plan et
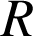 la rotation de centre
la rotation de centre
 et d'angle
et d'angle ![]() .
.
Déterminer l'écriture complexe de la composée ![]() et à l'aide des invariants, préciser la nature de
et à l'aide des invariants, préciser la nature de ![]() .
.
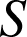 réflexion d'axe
réflexion d'axe ![]() a pour écriture complexe
a pour écriture complexe ![]() et
et
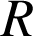 rotation de centre
rotation de centre
 et d'angle
et d'angle ![]() a pour écriture complexe
a pour écriture complexe 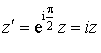 .
.
![]() a donc pour écriture complexe
a donc pour écriture complexe ![]() .
.
![]() ,
, ![]() et
et ![]() est invariant si et seulement si
est invariant si et seulement si ![]() , soit
, soit 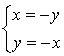 .
.
![]() est donc une similitude (produit de deux isométries) de rapport
est donc une similitude (produit de deux isométries) de rapport
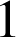 qui admet au moins 2 points invariants et n'est pas l'identité, c'est donc la réflexion d'axe la droite d'équation
qui admet au moins 2 points invariants et n'est pas l'identité, c'est donc la réflexion d'axe la droite d'équation ![]() .
.
Pour une représentation graphique, utilisez l'outil suivant.






