1)
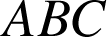un triangle dans le plan orienté. Les points
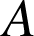et
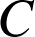ont respectivement pour images par la rotation
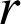de centre
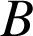et d'angle 
les points
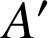et
.
Les points
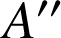et
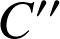sont respectivement les barycentres de 
et 
.
Après avoir déterminer l'homothétie
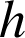telle que 
et 
, démontrer que les triangles
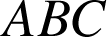et
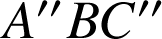sont semblables.
Pour une représentation graphique, utilisez l'outil suivant.
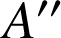et
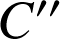sont respectivement les barycentres des systèmes 
et 
d'où :
pour tout point
, 
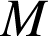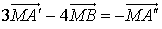soit pour 
, 
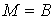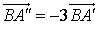,pour tout point
, 
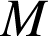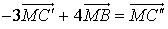soit pour , 
.
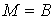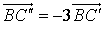Par l'homothétie
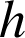de centre
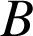et de rapport
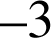, et
Le triangle
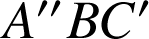' est donc l'image du triangle
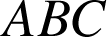par la composée 
{(
, 
et 
}.
La composée est une similitude de rapport
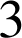, elle transforme donc un triangle en un triangle semblable. Les triangles
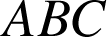et
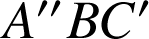' sont donc semblables.
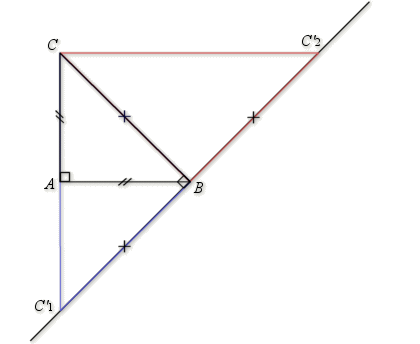
2)
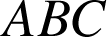est un triangle isocèle rectangle en
;
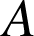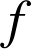est une similitude telle que 
et 
.
Déterminer
.
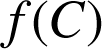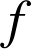est une similitude, elle transforme donc tout triangle en un triangle semblable.
Si 
, l'image du triangle
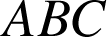est donc le triangle
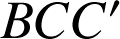isocèle et rectangle en
.
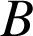est donc sur la perpendiculaire à
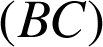passant par
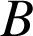et 
.
Il y a donc deux points images possibles 
et 
tel que
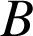milieu de 
; l'un correspond au cas où
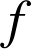conserve l'orientation des angles (
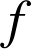est directe), et l'autre au cas où
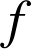transforme un angle en son opposé (
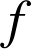est indirecte).
