1)
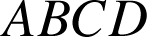est un rectangle tel que 
, 
(
) et
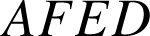est un carré de côté 1 tel que 
et 
.
On suppose qu'il existe une similitude
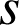telle que les images respectives de
,
,
,
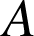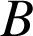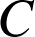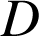soient
,
,
,
.
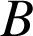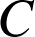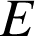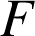Justifier qu'alors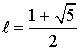 
.
Remarque : ce réel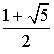 
est le nombre d'or, rapport de mesures privilégié par les artistes italiens de la Renaissance.
Par la similitude
: 
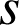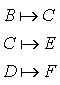donc 
(
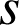conserve les rapports des distances).
d'où 
et 
.
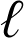est donc la solution positive de l'équation 
soit .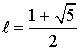
2) Le plan étant muni d'un repère orthonormal direct 
,
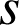est la transformation du plan qui au point
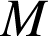de coordonnées
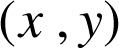associe le point
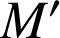de coordonnées
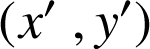telles que :
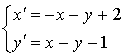
Justifier que
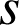est une similitude.
Pour une représentation graphique de la similitude, utilisez l'outil suivant.
Soit
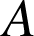et
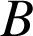d'images respectives
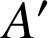et
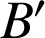par
.
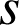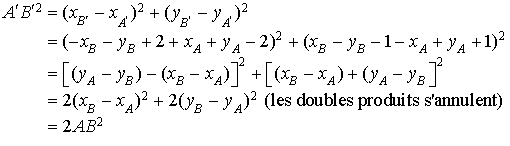
Soit 
.
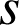est une transformation du plan qui multiplie les distances par
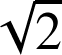, c'est une similitude de rapport
.
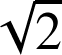