Par définition, une transformation 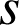du plan (bijection du plan dans lui-même) est une similitude si elle vérifie l'une des deux propriétés suivantes qui sont équivalentes :

• Quels que soient les points 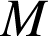, , 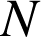, 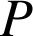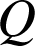( 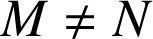, 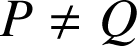) d'images respectives 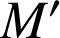, , 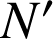, 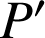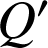par 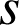, 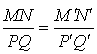(une similitude conserve les rapports des distances).

• Il existe un réel 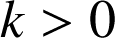tel que pour tous points 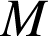, 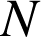d'images respectives 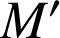, , 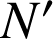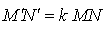(une similitude multiplie les distances par un réel 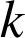). Le réel 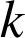est appelé rapport de la similitude.