Condition d'équilibre : équation du tétraèdre
Les conditions d'équilibre du milieu continu de volume τ et de frontière S s'écrivent :
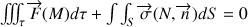
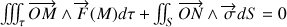
Avec M un point du volume et N un point de la surface.
Equation du tétraèdre
Pour un milieu continu, pour connaître la tension en un point N sur la surface S, il suffit de connaître les tensions sur les trois éléments de surfaces tri-rectangulaires passant par N.
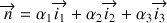
sont les cosinus directeurs de
.
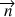On note σij densité superficielle de force, le premier indice indique l'axe perpendiculaire à la face considérée, le deuxième , l'axe sur lequel on projette la force.
Les forces de volume sont du 3ième ordre par rapport aux dimensions du tétraèdre, elles seront donc négligées.
La condition d'équilibre s'écrit :
Tenseur des contraintes
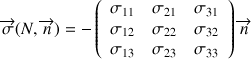
Ce terme représente le tenseur des contraintes et dépend linéairement de
. On montre que le moment résultant est nul ce qui implique que le tenseur des contraintes est symétrique, ce qui se traduit par :
σij = σji pour i différent de j
