Equilibre d'un fluide soumis à un réservoir
On considère un réservoir de liquide soumis à une accélération constante
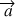horizontale.
Question
Trouver les surfaces isobares.
Indice
Il faut faire le bilan des forces et appliquer la relation fondamentale de la statique.
Solution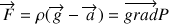
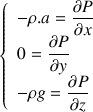
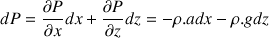
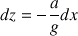
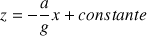
Commençons par écrire l'équation d'équilibre :
Le terme
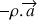correspond à la force d'inertie opposée à
.
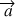Projetons cette relation sur le repère galiléen (Oxyz). On obtient de suite :
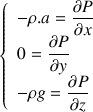
On a donc :
Les surfaces isobares sont telles que dP = 0. On a donc :
Après intégration, on obtient l'équation générale suivante :
Ces surfaces isobares sont bien orthogonales au vecteur F (propriété générale). La surface libre est aussi une surface isobare.
