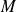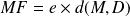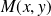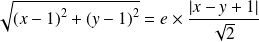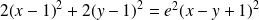Exo 21
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
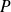 le plan affine euclidien rapporté à un repère orthonormé
le plan affine euclidien rapporté à un repère orthonormé
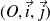 et un réel
et un réel
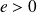 .
.
Soit
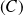 la conique de foyer
la conique de foyer
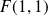 , d'excentricité
, d'excentricité
 et dont la directrice
et dont la directrice
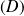 a pour équation :
a pour équation :
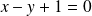 .
.
Question
On appelle courbe orthoptique de la conique
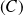 l'ensemble
l'ensemble
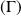 des points du plan d'où l'on peut mener deux tangentes à
des points du plan d'où l'on peut mener deux tangentes à
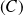 qui sont orthogonales.
qui sont orthogonales.
Question
On suppose que :
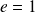 . Déterminer la courbe orthoptique de
. Déterminer la courbe orthoptique de
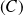 .
.
Paramétrez la conique et cherchez à quelle condition les tangentes en deux points
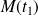 et
et
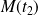 sont orthogonales.
sont orthogonales.
On suppose que
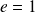 , donc la conique est une parabole.
, donc la conique est une parabole.
Son axe est la droite passant par
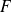 et orthogonale à
et orthogonale à
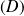 . Il coupe
. Il coupe
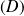 en un point
en un point
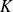 et le sommet
et le sommet
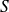 est le milieu de
est le milieu de
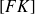 .
.
Le paramètre est la distance entre le foyer
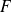 et la directrice
et la directrice
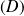 , donc :
, donc :
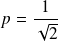 .
.
Donc la parabole a pour équation réduite
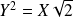 dans un repère
dans un repère
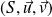 .
.
La parabole
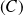 admet donc comme représentation paramétrique :
admet donc comme représentation paramétrique :
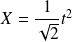 et
et
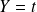 .
.
La tangente au point
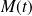 a pour vecteur directeur :
a pour vecteur directeur :
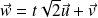 .
.
Donc les tangentes aux points
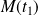 et
et
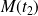 sont orthogonales si et seulement si :
sont orthogonales si et seulement si :
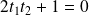 .
.
Donc la courbe orthoptique
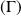 est l'ensemble des points
est l'ensemble des points
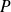 d'intersection des tangentes à la parabole aux points
d'intersection des tangentes à la parabole aux points
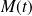 et
et
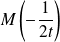 quand
quand
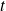 décrit
décrit
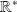 .
.
La tangente en
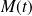 a pour équation :
a pour équation :
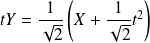 , donc
, donc
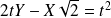 .
.
On en déduit la tangente en
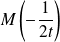 en remplaçant
en remplaçant
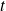 par
par
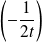 .
.
Son équation est :
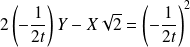 , donc :
, donc :
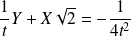 .
.
Donc
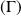 est l'ensemble des points
est l'ensemble des points
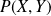 qui vérifient les deux équations.
qui vérifient les deux équations.
Donc :
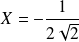 et
et
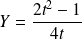 . Or quand
. Or quand
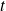 décrit
décrit
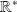 ,
,
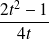 décrit
décrit
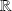 .
.
Donc
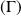 est la droite d'équation :
est la droite d'équation :
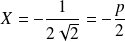 .
.
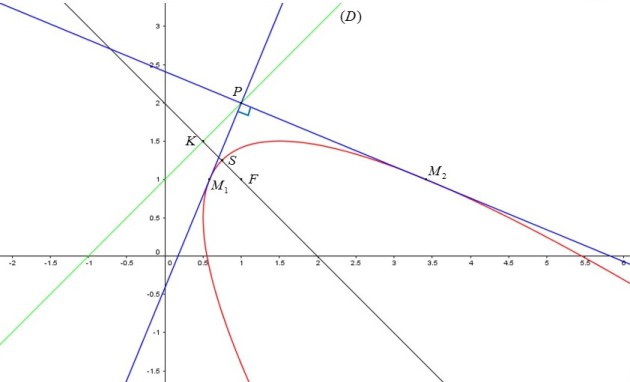
Conclusion : La courbe orthoptique de la parabole est sa directrice.
Remarque :
Ce résultat est vrai pour toutes les paraboles.
Question
On suppose que :
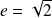 . Déterminer la courbe orthoptique de
. Déterminer la courbe orthoptique de
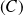 .
.
Paramétrez la conique et cherchez à quelle condition les tangentes en deux points
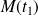 et
et
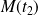 sont orthogonales.
sont orthogonales.
On suppose que
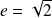 , donc la conique est une hyperbole.
, donc la conique est une hyperbole.
L'équation est :
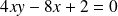 , donc :
, donc :
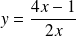 .
.
L'hyperbole
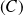 admet donc comme représentation paramétrique :
admet donc comme représentation paramétrique :
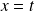 et
et
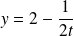 .
.
La tangente au point
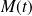 a pour vecteur directeur
a pour vecteur directeur
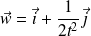 .
.
Donc les tangentes aux points
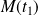 et
et
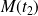 sont orthogonales si et seulement si :
sont orthogonales si et seulement si :
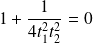 .
.
Cette équation n'admet pas de solution. On ne trouve jamais deux tangentes orthogonales.
Conclusion : La courbe orthoptique de l'hyperbole est l'ensemble vide.
Remarque :
La courbe orthoptique d'une hyperbole n'est pas toujours l'ensemble vide.
Si l'excentricité est inférieure à
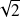 , la courbe orthoptique d'une hyperbole de centre
, la courbe orthoptique d'une hyperbole de centre
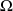 et d'équation réduite
et d'équation réduite
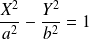 est le cercle de centre
est le cercle de centre
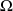 et de rayon
et de rayon
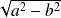 .
.
Question
On suppose que :
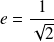 . Déterminer la courbe orthoptique de
. Déterminer la courbe orthoptique de
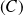 .
.
Paramétrez la conique et cherchez à quelle condition les tangentes en deux points
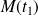 et
et
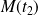 sont orthogonales.
sont orthogonales.
On suppose que :
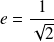 , donc la conique est une ellipse.
, donc la conique est une ellipse.
L'équation équivaut à :
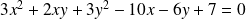 .
.
Les coordonnées du centre
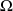 vérifient :
vérifient :
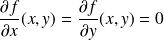 , donc :
, donc :
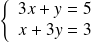 .
.
Donc le centre de l'ellipse est :
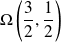 .
.
Et il existe un repère
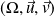 où l'équation de
où l'équation de
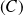 est :
est :
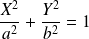 avec
avec
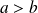 .
.
La distance entre
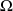 et
et
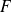 est :
est :
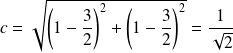 .
.
L'excentricité est :
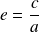 . Or :
. Or :
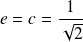 . Donc :
. Donc :
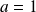 .
.
Et :
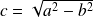 , donc
, donc
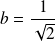 . Donc l'équation réduite est :
. Donc l'équation réduite est :
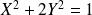 .
.
L'ellipse
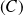 admet donc comme représentation paramétrique :
admet donc comme représentation paramétrique :
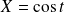 et
et
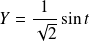 .
.
La tangente au point
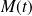 a pour vecteur directeur :
a pour vecteur directeur :
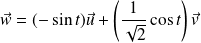 .
.
Les tangentes en
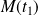 et
et
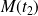 sont orthogonales si et seulement si :
sont orthogonales si et seulement si :
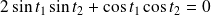 , donc si et seulement si :
, donc si et seulement si :
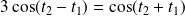 , donc si :
, donc si :
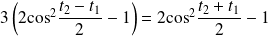 .
.
Or un point
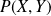 appartient à la courbe orthoptique
appartient à la courbe orthoptique
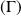 s'il est point d'intersection de deux tangentes orthogonales, donc si et seulement si il existe
s'il est point d'intersection de deux tangentes orthogonales, donc si et seulement si il existe
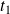 et
et
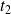 tels que :
tels que :
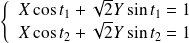 avec :
avec :
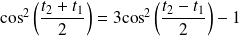 .
.
Le déterminant du système est :
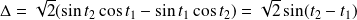 .
.
Il est non nul car
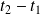 n'est pas un multiple de
n'est pas un multiple de
 sinon les tangentes seraient parallèles.
sinon les tangentes seraient parallèles.
Donc :
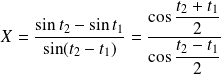 et :
et :
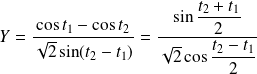 .
.
Donc :
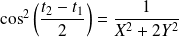 et
et
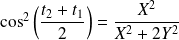 .
.
Donc
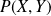 appartient à
appartient à
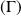 si et seulement si :
si et seulement si :
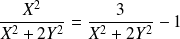 .
.
Donc la courbe orthoptique
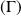 est le cercle d'équation :
est le cercle d'équation :
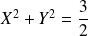 .
.
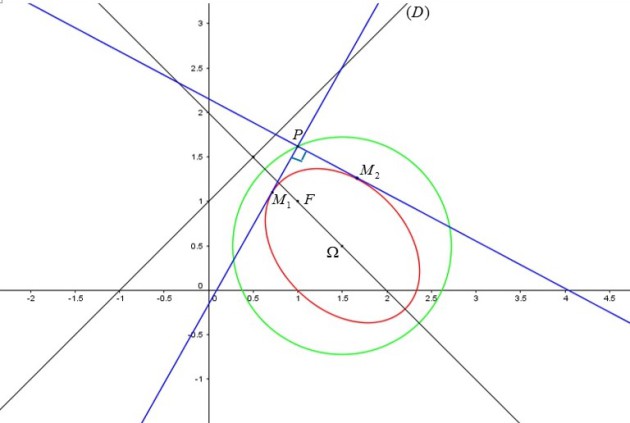
Conclusion : La courbe orthoptique de l'ellipse est le cercle de centre
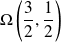 et de rayon
et de rayon
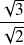 .
.
Remarque :
Plus généralement, la courbe orthoptique d'une ellipse de centre
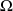 et d'équation réduite
et d'équation réduite
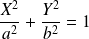 est le cercle de centre
est le cercle de centre
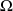 et de rayon
et de rayon
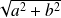 .
.