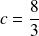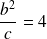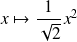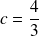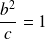Exo 18
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
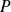 le plan affine euclidien rapporté à un repère orthonormé
le plan affine euclidien rapporté à un repère orthonormé
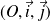 et un réel
et un réel
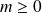 .
.
Soit
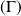 la conique d'équation :
la conique d'équation :
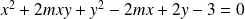 .
.
Question
Déterminer la nature de la conique
 suivant les valeurs de
suivant les valeurs de
 .
.
Déterminez son équation réduite.
Avec les notations du cours :
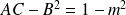 .
.
Donc la conique est dégénérée si et seulement si
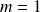 .
.
La matrice
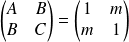 a pour valeurs propres
a pour valeurs propres
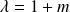 et
et
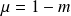 .
.
Elles sont distinctes si et seulement si
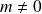 .
.
Si
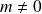 , le sous-espace propre associé à
, le sous-espace propre associé à
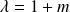 est la droite d'équation
est la droite d'équation
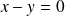 .
.
Et le sous-espace propre associé à
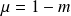 est la droite d'équation
est la droite d'équation
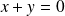 .
.
Donc on pose :
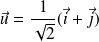 et
et
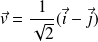 .
.
Soient
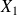 et
et
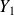 les coordonnées du point
les coordonnées du point
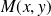 dans le repère
dans le repère
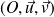 .
.
Donc :
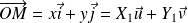 , donc :
, donc :
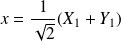 et
et
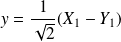 .
.
En remplaçant, on obtient l'équation de
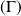 dans
dans
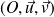 :
:
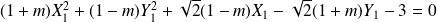 .
.
Si
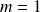 , l'équation équivaut à :
, l'équation équivaut à :
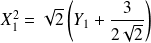 . Soit
. Soit
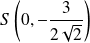 dans
dans
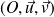 .
.
L'équation de
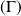 dans
dans
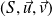 est :
est :
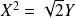 . Donc
. Donc
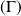 est une parabole.
est une parabole.
Si
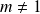 , l'équation équivaut à :
, l'équation équivaut à :
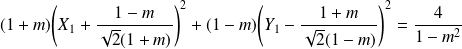 .
.
Soit
 le point de coordonnées
le point de coordonnées
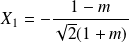 et
et
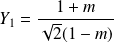 dans
dans
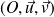 .
.
L'équation de
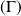 dans
dans
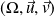 est :
est :
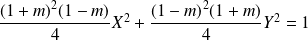 .
.
Si
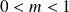 , les deux coefficients sont positifs, donc
, les deux coefficients sont positifs, donc
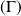 est une ellipse.
est une ellipse.
Si
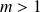 , les deux coefficients sont de signes contraires, donc
, les deux coefficients sont de signes contraires, donc
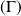 est une hyperbole.
est une hyperbole.
Si
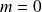 , l'équation est :
, l'équation est :
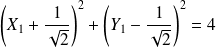 . Donc
. Donc
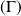 est un cercle.
est un cercle.
Conclusion : La conique
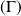 est un cercle si
est un cercle si
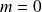 , une ellipse si
, une ellipse si
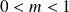 , une parabole si
, une parabole si
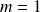 et une hyperbole si
et une hyperbole si
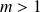 .
.
Question
Tracer la conique
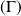 pour
pour
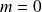 .
.
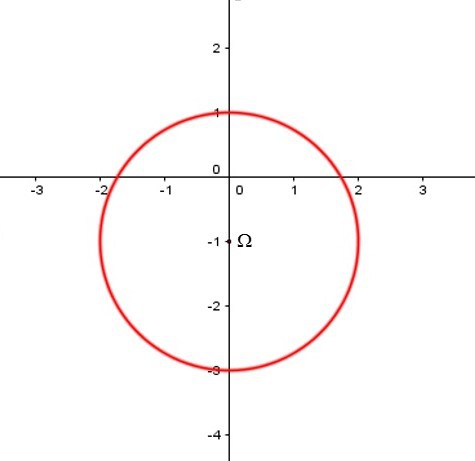
Si
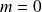 , la conique est un cercle.
, la conique est un cercle.
L'équation dans
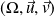 est :
est :
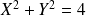 . Donc le centre est
. Donc le centre est
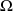 et le rayon est
et le rayon est
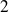 .
.
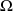 a pour coordonnées
a pour coordonnées
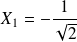 et
et
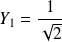 dans
dans
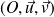 , donc
, donc
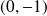 dans
dans
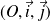 .
.
Conclusion : Si
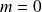 ,
,
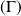 est le cercle de centre
est le cercle de centre
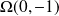 et de rayon
et de rayon
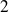 .
.
Question
Tracer la conique
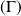 pour
pour
 .
.
A partir de l'équation réduite, calculez
 ,
,
 et
et
 , et utilisez les formules du cours.
, et utilisez les formules du cours.
Si
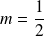 , la conique est une ellipse.
, la conique est une ellipse.
L'équation dans
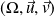 est :
est :
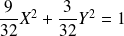 . Donc :
. Donc :
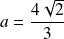 et
et
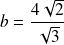 .
.
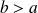 , donc :
, donc :
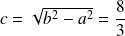 et l'excentricité est :
et l'excentricité est :
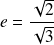 .
.
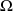 a pour coordonnées
a pour coordonnées
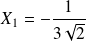 et
et
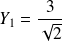 dans
dans
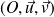 , donc
, donc
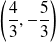 dans
dans
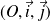 .
.
Pour tracer la courbe, on place le point
|
Les formules de changement de repère sont :
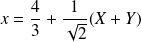 , et :
, et :
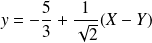 .
.
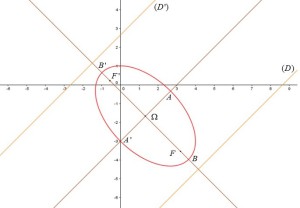
Conclusion : Si
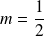 , la conique
, la conique
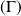 est une ellipse de centre
est une ellipse de centre
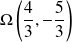 , d'excentricité
, d'excentricité
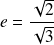 .
.
Ses sommets sont :
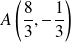 ,
,
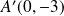 ,
,
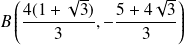 et
et
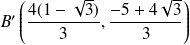 .
.
Ses foyers sont :
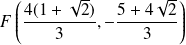 et
et
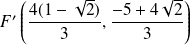 .
.
Les directrices associées ont pour équations :
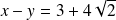 et
et
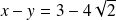 .
.
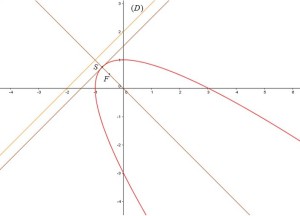
Question
Tracer la conique
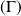 pour
pour
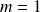 .
.
A partir de l'équation réduite, calculez
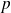 , et utilisez les formules du cours.
, et utilisez les formules du cours.
Si
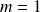 , la conique est une parabole.
, la conique est une parabole.
Le point
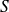 a pour coordonnées
a pour coordonnées
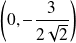 dans
dans
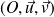 , donc
, donc
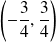 dans
dans
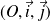 .
.
Et l'équation de
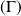 dans
dans
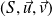 est :
est :
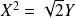 , donc
, donc
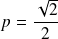 .
.
Pour tracer la courbe, on place le point
|
Les formules de changement de repère sont :
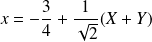 , et :
, et :
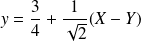 .
.
Conclusion : Si
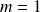 , la conique
, la conique
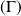 est une parabole de sommet
est une parabole de sommet
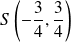 , d'axe d'équation
, d'axe d'équation
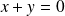 .
.
Son foyer est :
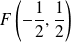 , et la directrice a pour équation :
, et la directrice a pour équation :
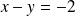 .
.
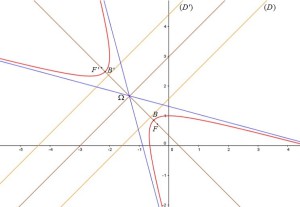
Question
Tracer la conique
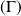 pour
pour
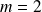 .
.
A partir de l'équation réduite, calculez
 ,
,
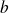 et
et
 , et utilisez les formules du cours.
, et utilisez les formules du cours.
Si
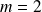 , la conique est une hyperbole.
, la conique est une hyperbole.
L'équation dans
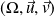 est :
est :
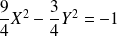 . Donc :
. Donc :
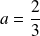 et
et
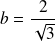 .
.
Donc :
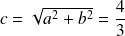 et l'excentricité est :
et l'excentricité est :
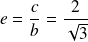 .
.
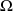 a pour coordonnées
a pour coordonnées
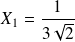 et
et
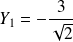 dans
dans
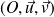 , donc
, donc
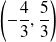 dans
dans
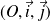 .
.
Pour tracer la courbe, on place le point
|
Les formules de changement de repère sont :
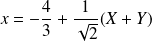 , et :
, et :
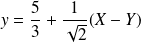 .
.
Conclusion : Si
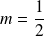 , la conique
, la conique
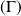 est une hyperbole de centre
est une hyperbole de centre
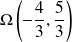 , d'excentricité
, d'excentricité
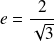 .
.
Ses sommets sont :
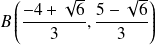 et
et
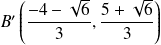 .
.
Ses foyers sont :
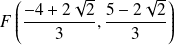 et
et
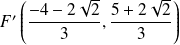 .
.
Les directrices associées ont pour équations
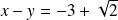 et
et
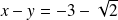 .
.
Les asymptotes ont pour équations
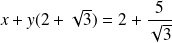 et
et
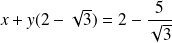 .
.