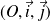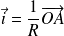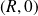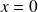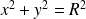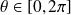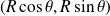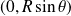Exo 20
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
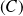un cercle de centre
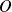et de rayon
.
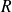Soit
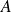un point de
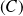et
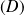la droite passant par
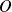et orthogonale à
.
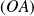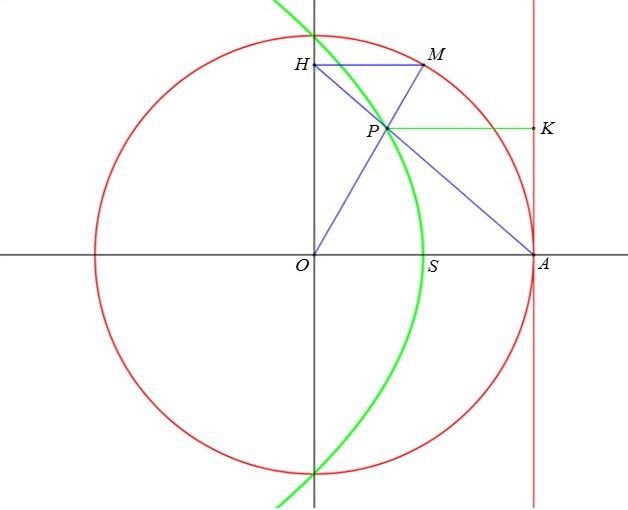
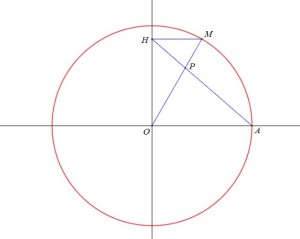
Pour tout point
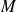de
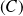, on construit son projeté orthogonal
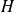sur
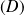et, s'il existe, le point
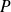intersection des droites
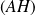et
.
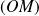Question
Déterminer le lieu de
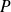lorsque
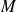décrit le cercle
.
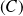Utilisez un paramétrage du cercle et déterminez une représentation polaire du lieu cherché.
On définit un repère orthonormé
Donc le point
Le cercle
Donc pour tout point
Son projeté orthogonal
|  |
La droite
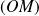a pour équation :
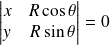, donc :
.
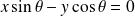La droite
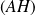a pour équation :
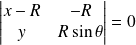, donc :
.
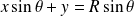Les droites
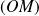et
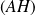sont sécantes si et seulement si :
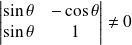, donc si et seulement si :
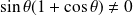, donc si
.
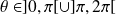Alors les coordonnées de
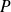sont solutions du système :
.
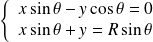Donc le point
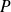a pour coordonnées :
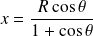et :
.
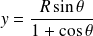Donc le lieu
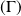de
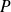a pour représentation polaire :
.
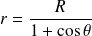Cette représentation est de la forme :
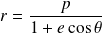avec
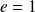et
.
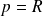Le lieu
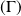est donc contenu dans une parabole.
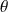décrit
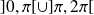, donc un seul point n'est pas atteint : le point
.
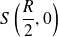Or :
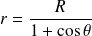équivaut à :
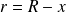, donc à
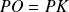si
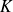est le projeté orthogonal de
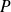sur la tangente en
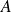au cercle.
Conclusion : Le lieu de
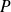est une parabole privée de son sommet
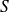. Le foyer est le centre
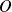du cercle et la directrice est la tangente en
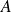au cercle
.
