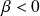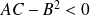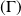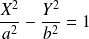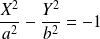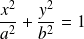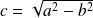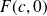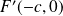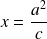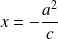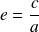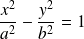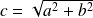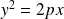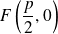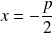Coniques
On suppose que le plan affine euclidien
 est rapporté à un repère orthonormal
est rapporté à un repère orthonormal
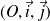 .
.
Définition :
Une conique est une courbe plane qui admet une équation de la forme :
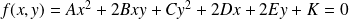 avec
avec
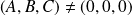 .
.
La conique est dégénérée si
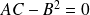 .
.
Donc, si
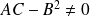 , on dira que la conique est non dégénérée.
, on dira que la conique est non dégénérée.
On peut remarquer qu'un cercle est une conique non dégénérée.
Fondamental :
La conique admet en tout point une tangente d'équation :
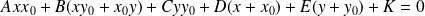 .
.
C'est un cas particulier de la tangente à une courbe implicite, mais la forme est adaptée à l'équation de la conique.
Exemple : Soit
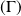 la conique d'équation
la conique d'équation
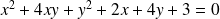 .
.
Le point
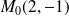 appartient à
appartient à
 et la tangente en
et la tangente en
 a pour équation :
a pour équation :
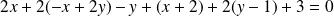 .
.
Donc la tangente à
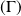 en
en
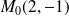 a pour équation :
a pour équation :
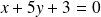 .
.
Fondamental :
Coniques non dégénérées (ou coniques à centre)
Soit
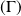 une conique non dégénérée.
une conique non dégénérée.
Il existe un unique point
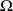 tel que
tel que
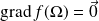 .
. Il existe un repère orthonormal
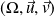 dans lequel l'équation de la conique est de la forme :
dans lequel l'équation de la conique est de la forme :
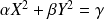 avec
avec
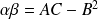 et
et
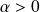 .
.Le point
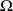 est centre de symétrie et les droites
est centre de symétrie et les droites
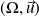 et
et
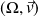 sont axes de symétrie de la conique
sont axes de symétrie de la conique
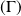 .
.Si
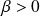 (donc
(donc
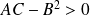 ), et :
), et :si
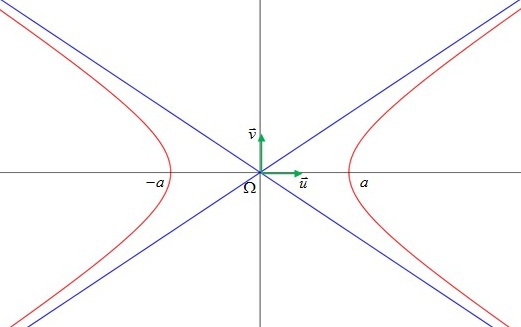
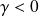 , alors :
, alors :
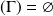 .
.si
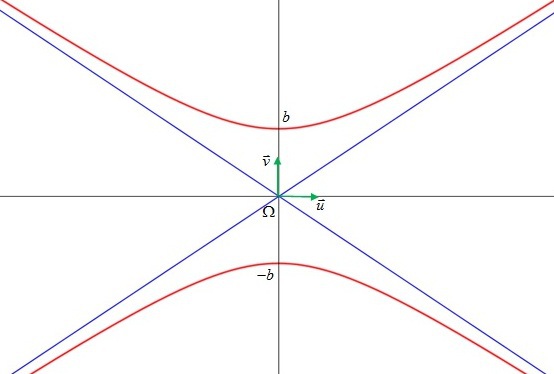
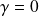 , alors :
, alors :
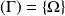 .
.si
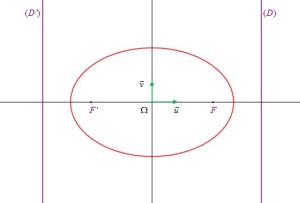
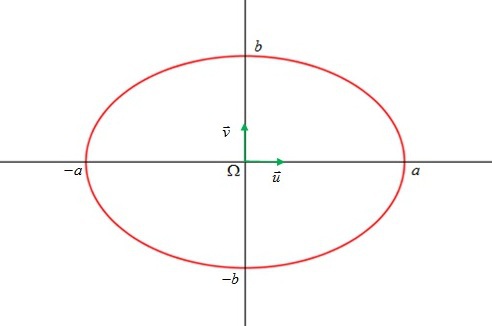
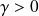 , alors
, alors
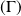 est une ellipse d'équation réduite :
est une ellipse d'équation réduite :
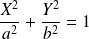 . [1]
. [1]
Les cercles sont des cas particuliers d'ellipses.
Les ellipses n'ont pas de branches infinies.
Les hyperboles ont deux asymptotes d'équations
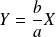 et
et
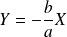 dans le repère
dans le repère
 .
.
Remarque :
Les deux derniers cas ne correspondent pas à deux types différents d'hyperbole : si l'on intervertit les vecteurs
 et
et
 , on passe d'un type d'équation à l'autre.
, on passe d'un type d'équation à l'autre.
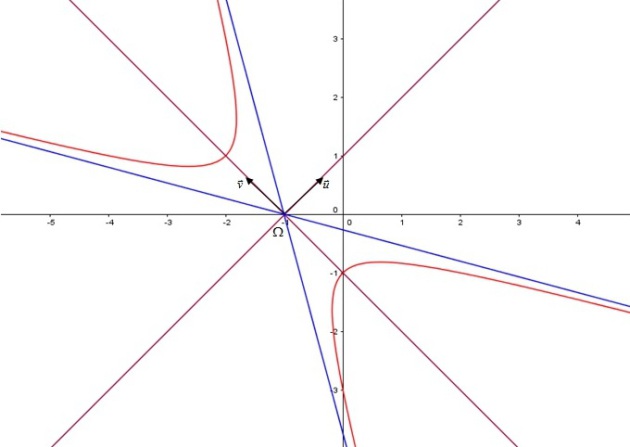
Dans l'exemple précédent, la conique
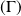 est non dégénérée car
est non dégénérée car
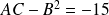 .
.
On commence par déterminer son centre
 .
.On pose :
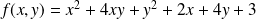 .
.Donc :
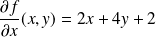 et
et
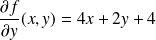 .
.Donc les coordonnées du centre sont solution du système :
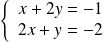 .
. Donc le centre de la conique est
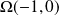 .
.Ensuite, on détermine le repère
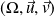 . Méthode
. MéthodeLa matrice
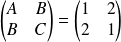 a pour valeurs propres
a pour valeurs propres
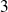 et
et
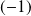 .
.Le sous-espace propre associé à
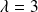 est la droite d'équation :
est la droite d'équation :
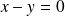 .
.Le sous-espace propre associé à
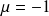 est la droite d'équation
est la droite d'équation
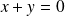 .
.On choisit donc les vecteurs
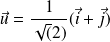 et
et
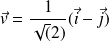 .
.Enfin, on détermine l'équation réduite.
Soient
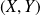 les coordonnées du point
les coordonnées du point
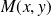 dans le repère
dans le repère
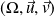 .
.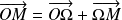 , donc
, donc
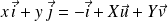 .
.Donc
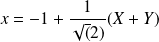 et
et
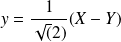 .
.En remplaçant dans l'équation de
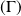 , on obtient :
, on obtient :
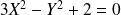 .
.Donc l'équation de
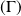 dans le repère
dans le repère
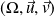 est :
est :
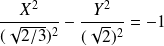 .
.Il s'agit donc d'une hyperbole de centre
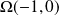 sous la seconde forme. Courbe[4].
sous la seconde forme. Courbe[4].Les asymptotes ont pour équations
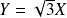 et
et
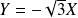 dans le repère
dans le repère
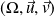 .
.Les points d'intersection avec l'axe
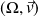 ont pour ordonnée
ont pour ordonnée
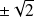 dans le repère
dans le repère
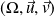 .
.
Fondamental :
Conique dégénérée
Soit
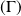 une conique dégénérée.
une conique dégénérée.
Il existe un repère dans lequel l'équation de la conique est de la forme :
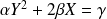 avec
avec
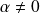 .
.Si
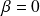 ,
,
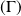 est
est
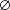 , ou une droite, ou la réunion de deux droites parallèles.
, ou une droite, ou la réunion de deux droites parallèles.Si
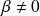 ,
,
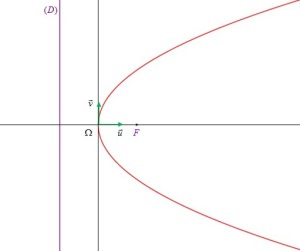
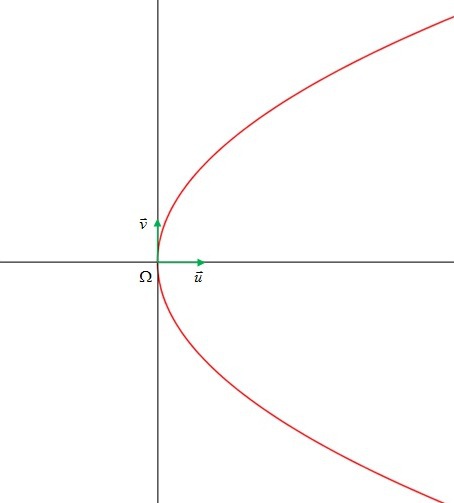
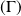 est une parabole d'équation réduite :
est une parabole d'équation réduite :
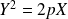 . [5]
. [5]
Suivant le choix des axes, on peut obtenir comme équation réduite d'une parabole
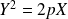 ou
ou
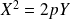 .
.
Exemple : Soit
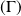 la conique d'équation
la conique d'équation
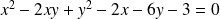 .
.
Il s'agit d'une conique dégénérée car
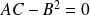 .
.
On détermine les vecteurs
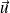 et
et
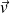 comme dans le cas précédent.
comme dans le cas précédent.La matrice
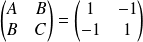 a pour valeurs propres
a pour valeurs propres
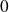 et
et
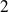 .
.Le sous-espace propre associé à
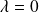 est la droite d'équation :
est la droite d'équation :
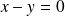 .
.Le sous-espace propre associé à
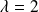 est la droite d'équation
est la droite d'équation
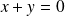 .
.On choisit donc les vecteurs
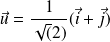 et
et
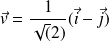 .
.On écrit l'équation dans le repère
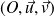 .
.Soient
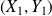 les coordonnées du point
les coordonnées du point
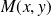 dans le repère
dans le repère
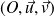 .
.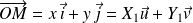 .
.Donc
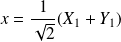 et
et
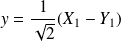 .
.En remplaçant dans l'équation de
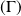 , on obtient :
, on obtient :
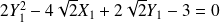 .
.Enfin, on détermine l'équation réduite.
L'équation équivaut à :
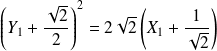 .
.Soit
 le point de coordonnées
le point de coordonnées
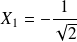 et
et
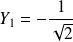 dans
dans
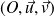 , donc
, donc
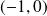 dans
dans
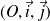 .
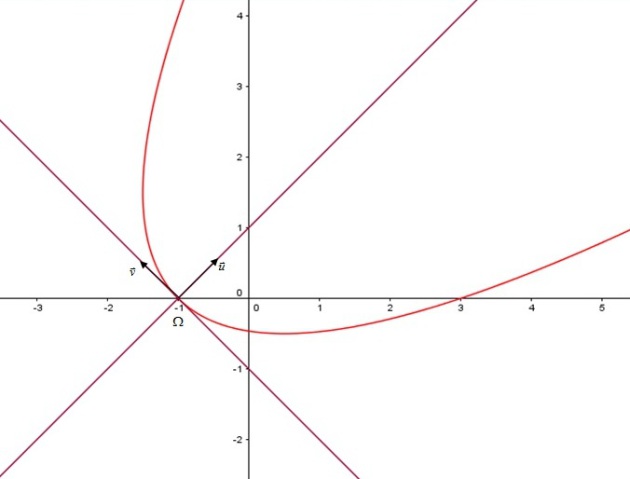
.Donc l'équation de
 est
est
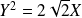 dans le repère
dans le repère
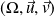 .
.Donc la courbe
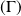 est une parabole de sommet
est une parabole de sommet
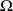 et d'axe
et d'axe
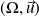 . Courbe[6].
. Courbe[6].
Fondamental :
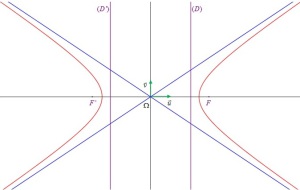
Définition monofocale
Soit une droite
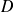 , un point
, un point
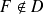 et un réel
et un réel
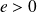 .
.
L'ensemble
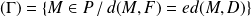 est une conique.
est une conique.
On dira qu'il s'agit de la conique de foyer
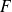 , de directrice
, de directrice
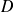 et d'excentricité
et d'excentricité
 .
.
C'est une ellipse (qui n'est pas un cercle) si
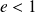 , une parabole si
, une parabole si
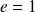 une hyperbole si
une hyperbole si
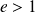 .
.
Conséquence : Il existe un repère dans lequel la représentation polaire de la conique est de la forme :
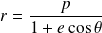 .
.
La réciproque est vraie : toutes les ellipses (sauf les cercles), les paraboles et les hyperboles peuvent être définies de cette façon.
Fondamental :
Si
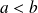 , il suffit d'intervertir l'abscisse et l'ordonnée (et donc
, il suffit d'intervertir l'abscisse et l'ordonnée (et donc
 et
et
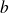 ) dans les formules précédentes.
) dans les formules précédentes.
Fondamental :
Si l'équation est
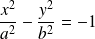 , il suffit d'intervertir l'abscisse et l'ordonnée (et donc
, il suffit d'intervertir l'abscisse et l'ordonnée (et donc
 et
et
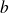 ) dans les formules précédentes.
) dans les formules précédentes.
Fondamental :
Si l'équation est
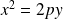 , il suffit d'intervertir l'abscisse et l'ordonnée dans les formules précédentes.
, il suffit d'intervertir l'abscisse et l'ordonnée dans les formules précédentes.
Fondamental :
Définition bifocale
Soient
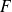 et
et
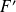 deux points distincts.
deux points distincts.
L'ensemble
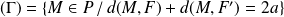 est une ellipse de foyers
est une ellipse de foyers
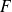 et
et
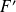 si
si
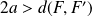 .
.L'ensemble
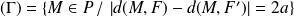 est une hyperbole de foyers
est une hyperbole de foyers
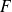 et
et
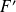 si
si
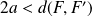 .
.
Réciproquement, toute ellipse (autre qu'un cercle) et toute hyperbole peut être définie sous forme bifocale.