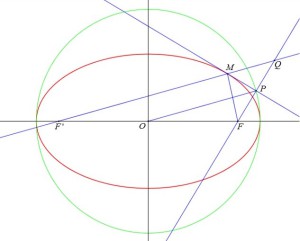
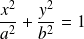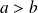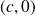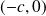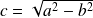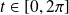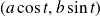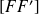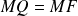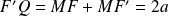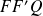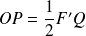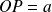Exo 19
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
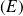une ellipse de foyers
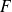et
.
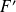Pour tout point
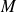de
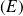, on appelle
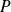le projeté orthogonal de
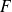sur la tangente en
.
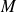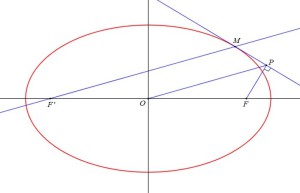
Question
Démontrer que la droite
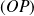est parallèle à la droite
.
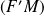Utilisez un paramétrage de l'ellipse.
L'ellipse
Donc il existe un repère de centre
Les foyers
Pour tout point
|  |
La tangente en
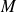a pour équation :
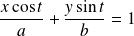, donc :
.
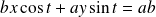Le vecteur
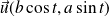est normal à la tangente, donc
est colinéaire à
.
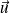Donc l'équation de
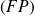est :
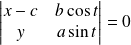, donc :
.
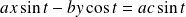Donc les coordonnées
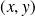de
vérifient le système :
.
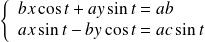Le déterminant du système est :
.
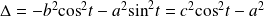Or :
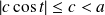. Donc :
.
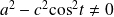Donc :
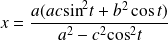et
.
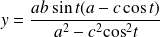Or :
.
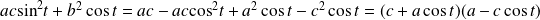Donc le point
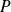a pour coordonnées :
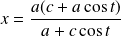et :
.
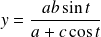Donc
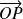est colinéaire à
.
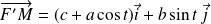Conclusion : La droite
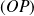est parallèle à la droite
.
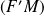Question
En déduire le lieu
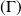du point
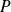lorsque le point
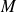décrit l'ellipse
.
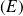Utilisez la définition bifocale de l'ellipse.
La droite
Donc elle coupe la droite
Donc la tangente en
Donc :
Or dans le triangle
|  |
Conclusion : Le lieu du point
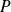est le cercle dont le centre est le centre de l'ellipse et de rayon égal au demi-grand axe de l'ellipse.
Ce cercle est appelé cercle principal de l'ellipse.
Remarque :
Le triangle
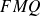est isocèle, donc la tangente à l'ellipse est à la fois médiatrice de
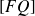, et bissectrice intérieure de l'angle
.
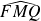Conséquence : La tangente en
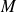à l'ellipse est bissectrice extérieure de l'angle
.
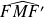