Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
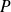 de repère orthonormé
de repère orthonormé
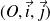 .
.
Soit
 la courbe d'équation :
la courbe d'équation :
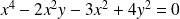 .
.
Question
Etudier les symétries de la courbe
 .
.
Soit
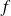 la fonction définie par :
la fonction définie par :
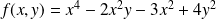 .
.
On remarque que :
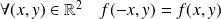 .
.
Conclusion : La courbe
 est symétrique par rapport à l'axe des ordonnées.
est symétrique par rapport à l'axe des ordonnées.
Question
Montrer que la courbe
 est incluse dans une partie bornée du plan.
est incluse dans une partie bornée du plan.
Ramenez vous à des équations du second degré.
L'équation de
 peut s'écrire :
peut s'écrire :
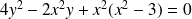 .
.
C'est une équation du second degré en
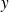 .
.
Son discriminant :
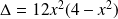 est négatif si et seulement si
est négatif si et seulement si
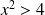 . Alors l'équation n'aura pas de solution.
. Alors l'équation n'aura pas de solution.
Donc tous les points de la courbe
 vérifient :
vérifient :
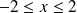 .
.
En posant
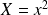 , l'équation de
, l'équation de
 s'écrit :
s'écrit :
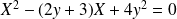 .
.
C'est une équation du second degré en
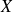 de discriminant :
de discriminant :
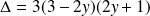 .
.
Il est négatif si et seulement si
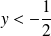 ou
ou
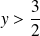 . Alors l'équation n'aura pas de solution.
. Alors l'équation n'aura pas de solution.
Donc tous les points de la courbe
 vérifient :
vérifient :
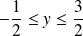 .
.
Donc la courbe
 est incluse dans
est incluse dans
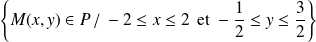 .
.
Conclusion : La courbe
 est incluse dans une partie bornée du plan.
est incluse dans une partie bornée du plan.
La courbe
 n'admet donc pas de branche infinie.
n'admet donc pas de branche infinie.
Question
Déterminer les points stationnaires de
 et préciser leur tangente.
et préciser leur tangente.
Résolvez l'équation :
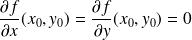 .
.
Puis étudiez la limite de
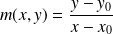 quand
quand
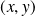 tend vers
tend vers
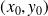 .
.
La fonction
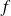 est polynômiale, donc de classe
est polynômiale, donc de classe
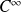 sur
sur
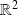 .
.
Ses dérivées partielles sont :
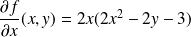 et
et
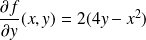 .
.
Un point est stationnaire si et seulement si :
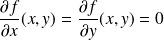 .
.
Or :
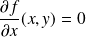 si et seulement si
si et seulement si
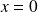 ou
ou
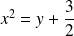 , avec
, avec
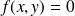 .
.
Si
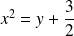 , alors :
, alors :
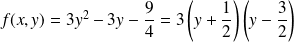 .
.
Donc :
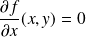 si et seulement si
si et seulement si
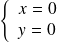 ou
ou
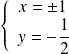 ou
ou
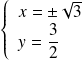 .
.
Et :
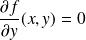 si et seulement si
si et seulement si
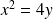 avec
avec
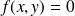 .
.
Or, si
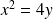 , alors
, alors
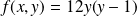 .
.
Donc :
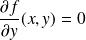 si et seulement si
si et seulement si
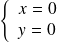 ou
ou
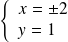 .
.
Conclusion : La courbe
 admet un unique point stationnaire, le point
admet un unique point stationnaire, le point
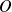 .
.
Pour obtenir les tangentes au point
 , il faut étudier la limite de
, il faut étudier la limite de
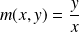 quand
quand
 et
et
 tendent vers
tendent vers
 avec
avec
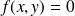 .
.
Si
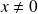 , l'équation de
, l'équation de
 peut s'écrire :
peut s'écrire :
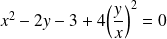 .
.
Si
 et
et
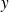 tendent vers
tendent vers
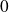 , alors
, alors
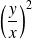 tend vers
tend vers
 , donc
, donc
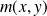 tend vers
tend vers
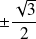 .
.
Conclusion : Au point
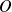 , deux branches de la courbe
, deux branches de la courbe
 se coupent, l'une avec une tangente de pente
se coupent, l'une avec une tangente de pente
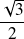 , l'autre avec une tangente de pente
, l'autre avec une tangente de pente
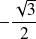 .
.
Question
Préciser les points réguliers de
 où la tangente est horizontale ou verticale.
où la tangente est horizontale ou verticale.
Résolvez les équations
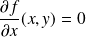 et
et
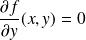 .
.
La courbe
 admet un unique point stationnaire, le point
admet un unique point stationnaire, le point
 .
.
Conclusion : Tous les points de
 sauf le point
sauf le point
 sont réguliers.
sont réguliers.
La tangente en
 est horizontale si
est horizontale si
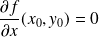 et
et
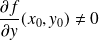 .
.
Conclusion : Il y a une tangente horizontale en quatre points
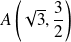 ,
,
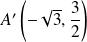 ,
,
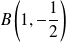 et
et
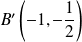 .
.
La tangente en
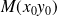 est verticale si
est verticale si
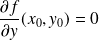 et
et
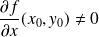 .
.
Conclusion : Il y a une tangente verticale en deux points
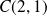 et
et
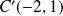 .
.
Question
Etudier suivant les valeurs de
 et
et
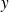 le signe du coefficient directeur de la tangente pour les autres points réguliers de
le signe du coefficient directeur de la tangente pour les autres points réguliers de
 .
.
Utilisez l'équation de la tangente en un point régulier.
Le coefficient directeur de la tangente en
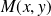 est :
est :
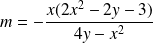 .
.
Donc
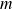 est du signe de :
est du signe de :
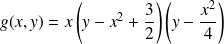 .
.
Ce signe dépend de la position du point
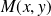 par rapport à l'axe des ordonnées et par rapport aux deux paraboles d'équations
par rapport à l'axe des ordonnées et par rapport aux deux paraboles d'équations
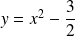 et
et
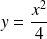 .
.
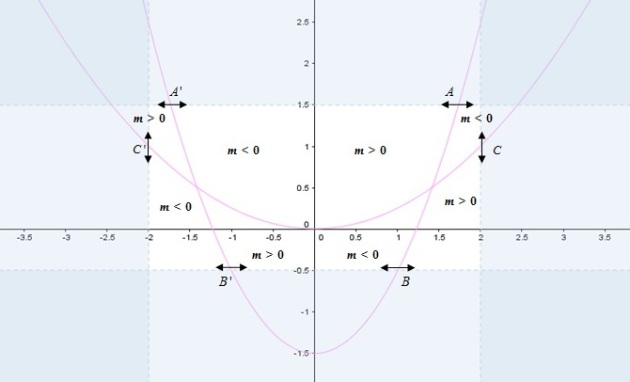
Question
En déduire l'allure de la courbe
 .
.
La branche de
 qui a pour pente
qui a pour pente
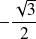 au point
au point
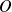 « descend » du point
« descend » du point
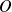 au point
au point
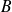 car
car
 augmente et
augmente et
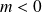 , donc
, donc
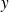 diminue.
diminue.
Puis
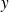 augmente car il n'y a pas de point en dessous de
augmente car il n'y a pas de point en dessous de
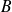 et
et
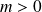 , donc
, donc
 augmente. Donc la courbe « monte » jusqu'au point
augmente. Donc la courbe « monte » jusqu'au point
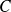 .
.
Ensuite,
 diminue car il n'y a pas de point à droite de
diminue car il n'y a pas de point à droite de
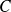 , et
, et
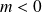 , donc
, donc
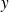 augmente. Donc la courbe « monte » jusqu'au point
augmente. Donc la courbe « monte » jusqu'au point
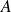 .
.
Ensuite,
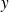 diminue car il n'y a pas de point au dessus de
diminue car il n'y a pas de point au dessus de
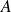 , et
, et
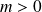 , donc
, donc
 diminue. Donc la courbe « descend » jusqu'au point
diminue. Donc la courbe « descend » jusqu'au point
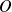 qu'elle atteint avec une pente de
qu'elle atteint avec une pente de
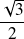 .
.
Le reste de la courbe est obtenu par symétrie par rapport à l'axe des ordonnées.
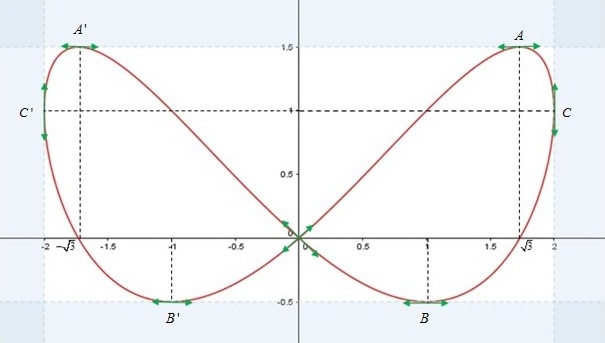
On peut préciser la position de la courbe par rapport à ses tangentes en
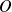 .
.
En effet, l'équation de
 peut s'écrire :
peut s'écrire :
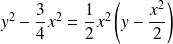 .
.
Donc
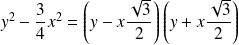 est du signe de
est du signe de
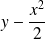 .
.
Il dépend donc de la position de la courbe par rapport à la parabole d'équation
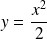 .
.
Au voisinage du point
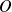 :
:
si
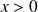 et
et
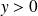 :
:
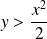 et
et
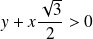 , donc
, donc
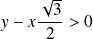 .
.si
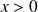 et
et
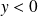 :
:
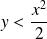 et
et
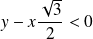 , donc
, donc
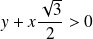 .
.si
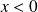 et
et
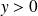 :
:
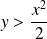 et
et
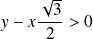 , donc
, donc
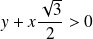 .
.si
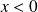 et
et
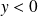 :
:
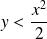 et
et
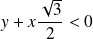 , donc
, donc
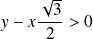 .
.
Conclusion : La courbe
 est au dessus de ses tangentes au point
est au dessus de ses tangentes au point
 .
.
On peut remarquer que cela implique l'existence de deux points d'inflexion
 et
et
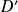 symétriques par rapport à l'axe des ordonnées et situés dans le demi-plan
symétriques par rapport à l'axe des ordonnées et situés dans le demi-plan
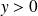 .
.





