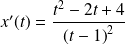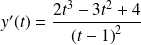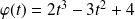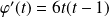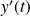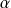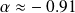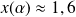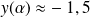Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
 de repère orthonormé
de repère orthonormé
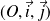 .
.
Soit
 la courbe d'équation :
la courbe d'équation :
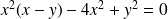 .
.
Question
Déterminer une représentation polaire de la courbe
 .
.
Posez :
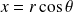 et
et
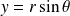 .
.
On remarque que si
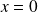 , alors
, alors
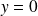 , et que si
, et que si
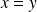 , alors
, alors
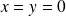 .
.
Donc pour tout point
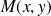 distinct de
distinct de
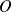 , on a :
, on a :
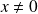 et
et
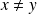 .
.
Donc la courbe
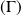 passe par le point
passe par le point
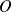 et ne coupe l'axe des ordonnées et la première bissectrice qu'en ce point.
et ne coupe l'axe des ordonnées et la première bissectrice qu'en ce point.
Pour tout point
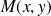 distinct de
distinct de
 , on pose :
, on pose :
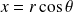 et
et
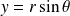 .
.
L'équation devient :
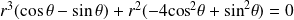 .
.
Donc
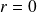 ou
ou
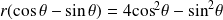 . Or
. Or
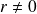 car
car
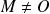 .
.
Et
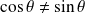 , puisque le point
, puisque le point
 n'appartient pas à la première bissectrice.
n'appartient pas à la première bissectrice.
Donc un point
 appartient à
appartient à
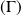 si et seulement si
si et seulement si
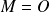 ou
ou
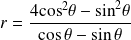 .
.
On retrouve le point
 si
si
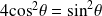 , donc si
, donc si
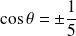 .
.
Conclusion : La courbe
 est la courbe de représentation polaire :
est la courbe de représentation polaire :
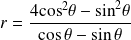 .
.
Question
Déterminer une représentation paramétrique cartésienne de la courbe
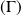 .
.
Posez :
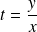 .
.
Pour tout point
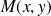 distinct de
distinct de
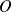 , on a
, on a
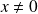 , donc on pose :
, donc on pose :
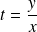 .
.
Alors
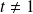 puisque
puisque
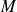 n'est pas sur la première bissectrice.
n'est pas sur la première bissectrice.
L'équation devient :
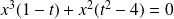 , donc :
, donc :
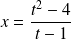 , et :
, et :
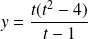 .
.
Donc un point
 appartient à
appartient à
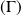 si et seulement si
si et seulement si
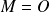 ou
ou
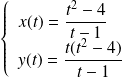 .
.
Pour
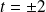 , on retrouve le point
, on retrouve le point
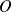 .
.
Conclusion : La courbe
 est la courbe de représentation paramétrique :
est la courbe de représentation paramétrique :
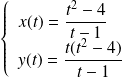 .
.
Question
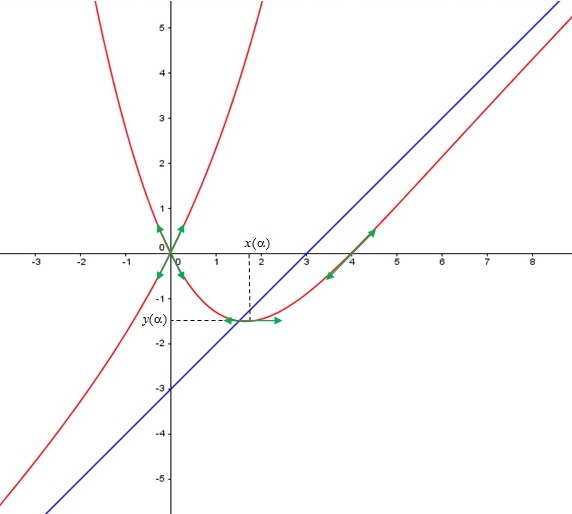
Construire la courbe
 .
.
Choisissez l'un des deux paramétrages pour construire la courbe.
Le paramétrage cartésien semble plus simple pour l'étude de la courbe
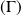 .
.
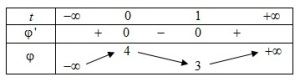
La courbe admet des branches infinies lorsque
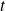 tend vers
tend vers
 ou vers l'infini.
ou vers l'infini.
Or :
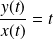 . Donc lorsque
. Donc lorsque
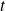 tend vers l'infini, il y a une branche parabolique de direction
tend vers l'infini, il y a une branche parabolique de direction
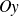 .
.
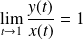 et
et
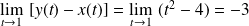 .
.
Donc lorsque
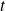 tend vers
tend vers
 , il y a une asymptote oblique d'équation
, il y a une asymptote oblique d'équation
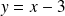 .
.
La courbe est au dessus quand
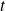 tend vers
tend vers
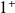 et en dessous quand
et en dessous quand
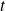 tend vers
tend vers
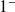 .
.
Et :
Si l'on pose
Donc
Donc :
|
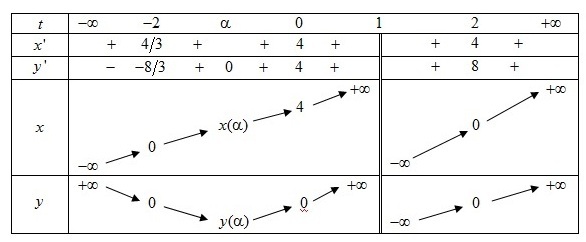
On en déduit la courbe.