Exo 15
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le plan affine euclidien
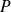de repère orthonormé
.
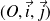Soit
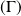la courbe d'équation :
.
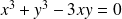Question
Etudier les symétries de la courbe
.
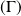Soit
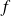la fonction définie par :
.
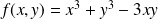On remarque que :
.
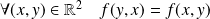Conclusion : La courbe
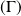est symétrique par rapport à la première bissectrice.
Question
Déterminer, suivant la valeur du réel
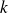, le nombre de points d'intersection de la courbe
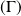avec la droite
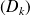d'équation
.
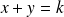En déduire la localisation de la courbe.
Etudiez le signe du discriminant de l'équation obtenue.
Ensuite, pour préciser un peu mieux la localisation, comparez les signes de
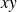et de
.
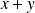L'abscisse des points d'intersection la courbe
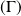avec la droite
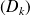vérifie :
.
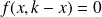Donc :
.
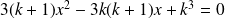Si
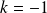, l'équation n'a pas de solution.
Si
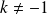, le discriminant est :
.
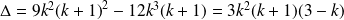Conclusion : Si
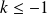ou
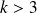, il n'y a pas de point d'intersection. Si
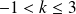, il y a deux points d'intersection (symétriques par rapport à la première bissectrice). Ils sont confondus pour
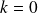et pour
.
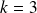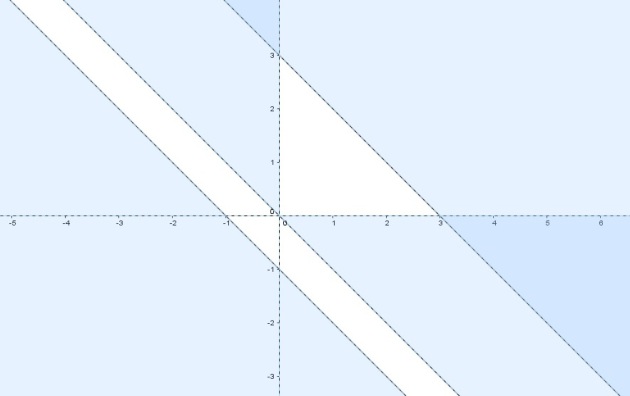
Donc la courbe
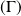est incluse dans la partie de plan
.
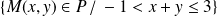On peut aussi remarquer que :
.
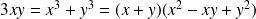Or le polynôme
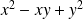est toujours positif ou nul. Donc
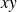est du signe de
.
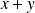Il n'y a donc pas de points de la courbe si
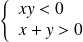ou si
.
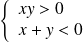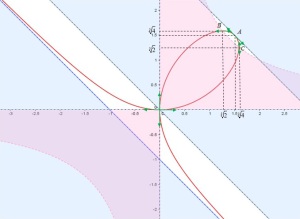
Conclusion : La courbe
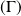est incluse dans la partie blanche[1].
Question
En déduire les branches infinies de la courbe
.
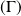Déterminez les abscisses des points d'intersection de la courbe avec
.
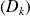On a vu que pour tout
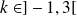, la droite
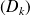coupe
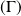en deux points symétriques par rapport à la première bissectrice.
On a donc
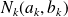et
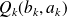avec
.
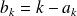Leur abscisse est solution de l'équation :
.
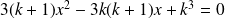Donc :
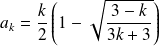et
.
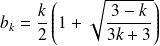Donc pour avoir une branche infinie, il faut que
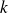tende vers
.
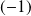Et si
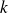tend vers
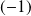, alors
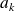tend vers
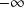et
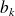tend vers
.
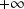Conclusion : La courbe
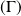admet une asymptote oblique d'équation
.
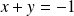Elle se trouve au dessus de son asymptote.
Question
Déterminer les points stationnaires de
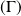et préciser leur tangente.
Résolvez l'équation :
.
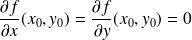Puis étudiez la limite de
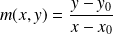quand
tend vers
.
La fonction
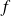est polynômiale, donc de classe
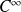sur
.
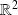Ses dérivées partielles sont :
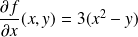et
.
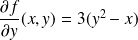Donc :
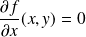si et seulement si
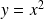avec
.
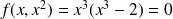Donc :
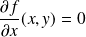si et seulement si
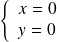ou
.
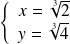Par symétrie :
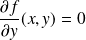si et seulement si
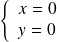ou
.
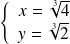Conclusion : La courbe
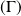admet un unique point stationnaire, le point
.
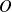Etant donnée l'étude précédente, il y a deux branches de
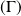qui se coupent en
.
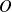Elles sont symétriques par rapport à la première bissectrice.
Pour obtenir les tangentes au point
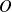, il faut étudier la limite de
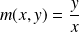quand
et
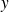tendent vers
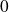avec
.
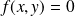Si
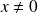, l'équation peut s'écrire :
.
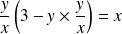Donc, si
tend vers
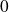, alors
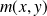tend vers
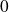ou
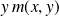tend vers
.
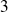Donc
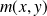tend vers
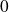ou
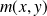tend vers l'infini car
.
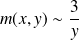Conclusion : Au point
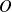, deux branches de
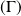se coupent, l'une avec une tangente horizontale, l'autre avec une tangente verticale.
Question
Préciser les points réguliers de
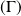où la tangente est horizontale ou verticale.
Résolvez les équations
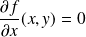et
.
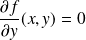La courbe
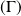admet un unique point stationnaire, le point
.
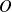Donc tous les points de
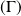sauf le point
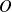sont réguliers.
La tangente en
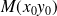(distinct de
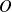) a pour équation :
.
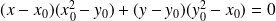Or :
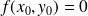. Donc l'équation de la tangente est :
.
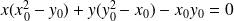La tangente est horizontale si
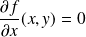et
.
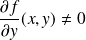La tangente est verticale si
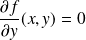et
.
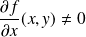Conclusion : Il y a une tangente horizontale en
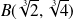et une tangente verticale en
.
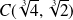La courbe
est tangente en
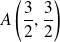à la droite d'équation
.
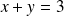Question
Etudier suivant les valeurs de
et
le signe du coefficient directeur de la tangente pour les autres points réguliers de
.
En déduire l'allure de la courbe
.
Utilisez l'équation de la tangente en un point régulier.
Le coefficient directeur de la tangente en
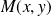est :
.
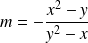Il est donc du signe de
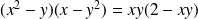car
.
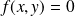Conclusion :
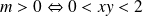et
.
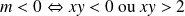Dans la partie bleue, il n'y a pas de points de la courbe
Dans la partie rose, la pente est positive, et dans la partie blanche elle est négative. La branche qui part de l'asymptote en
Le reste de la courbe est obtenu par symétrie par rapport à la première bissectrice. On obtient ainsi l'allure de la courbe
|  |
