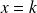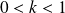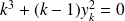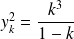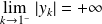Etude d'une courbe plane définie sous forme implicite
On suppose que le plan affine euclidien
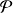 est rapporté à un repère orthonormal
est rapporté à un repère orthonormal
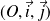 .
.
Définition :
Une courbe implicite du plan est définie par la donnée d'un ouvert
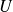 non vide de
non vide de
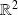 et d'une fonction
et d'une fonction
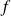 de classe
de classe
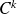 de
de
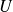 dans
dans
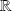 avec
avec
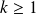 .
.
La courbe
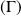 est l'ensemble des points
est l'ensemble des points
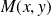 du plan tels que
du plan tels que
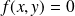 .
.
Exemple : Dans le plan affine euclidien
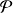 de repère orthonormé
de repère orthonormé
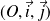 , on considère la courbe
, on considère la courbe
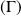 d'équation :
d'équation :
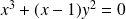 .
.
Méthode :
La première idée pour construire la courbe définie sous forme implicite peut être :
de se ramener à l'étude d'une fonction.
de paramétrer la courbe sous forme cartésienne.
de paramétrer la courbe sous forme polaire.
Méthode :
On peut aussi l'étudier directement sous forme implicite.
Ce qui suit est l'étude de l'exemple précédent sous forme implicite.
Fondamental :
Recherche des symétries
Si
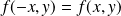 pour tout point
pour tout point
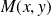 de
de
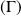 , alors la courbe est symétrique par rapport à l'axe des ordonnées.
, alors la courbe est symétrique par rapport à l'axe des ordonnées.Si
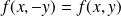 pour tout point
pour tout point
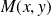 de
de
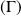 , alors la courbe est symétrique par rapport à l'axe des abscisses.
, alors la courbe est symétrique par rapport à l'axe des abscisses.Si
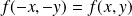 pour tout point
pour tout point
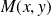 de
de
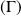 , alors la courbe est symétrique par rapport au point
, alors la courbe est symétrique par rapport au point
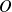 .
.Si
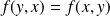 pour tout point
pour tout point
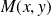 de
de
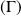 , alors la courbe est symétrique par rapport à la première bissectrice d'équation
, alors la courbe est symétrique par rapport à la première bissectrice d'équation
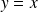 .
.
Dans l'exemple précédent, on a :
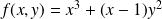 . Donc :
. Donc :
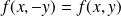 pour tout couple
pour tout couple
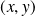 de
de
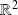 .
.
Donc la courbe
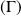 est symétrique par rapport à l'axe des abscisses.
est symétrique par rapport à l'axe des abscisses.
Méthode :
Localiser la courbe, c'est-à-dire rechercher les parties du plan ne contenant pas de points de la courbe permettra de simplifier les études suivantes.
Dans l'exemple précédent, l'équation s'écrit :
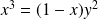 , donc :
, donc :
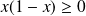 , donc :
, donc :
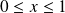 .
.
De plus, aucun couple de la forme
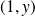 n'est solution de l'équation.
n'est solution de l'équation.
Donc la courbe
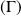 est incluse dans la partie de plan :
est incluse dans la partie de plan :
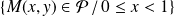 .
.
Définition :
Un point
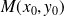 de
de
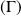 est régulier si
est régulier si
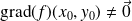 .
.
Sinon le point
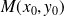 de
de
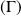 est stationnaire.
est stationnaire.
Dans l'exemple précédent, la fonction
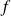 est polynômiale, donc de classe
est polynômiale, donc de classe
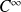 sur
sur
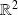 .
.
Ses dérivées partielles sont :
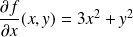 et
et
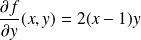 .
.
Donc :
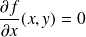 si et seulement si
si et seulement si
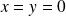 .
.
Et :
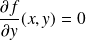 si et seulement si
si et seulement si
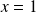 ou
ou
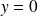 .
.
Or il n'y a aucun point de
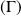 tel que
tel que
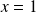 . Et si
. Et si
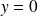 , alors
, alors
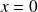 .
.
Donc la courbe
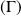 admet un unique point stationnaire, le point
admet un unique point stationnaire, le point
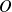 . Tous les autres points sont réguliers.
. Tous les autres points sont réguliers.
Fondamental :
Etude en un point régulier
Si le point
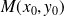 est régulier, la courbe admet en
est régulier, la courbe admet en
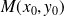 une tangente orthogonale à
une tangente orthogonale à
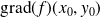 .
.
L'équation de la tangente est donc :
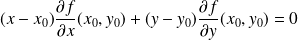 .
.
Donc la tangente est horizontale si et seulement si
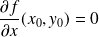 .
.
Et la tangente est verticale si et seulement si :
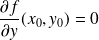 .
.
Dans l'exemple précédent, pour tout point
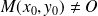 de
de
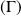 :
:
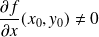 et
et
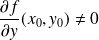 .
.
Donc il n'y a ni point à tangente horizontale, ni point à tangente verticale.
La tangente en
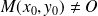 a pour coefficient directeur :
a pour coefficient directeur :
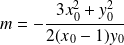 .
.
Or pour tout point
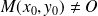 de la courbe, on a :
de la courbe, on a :
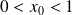 .
.
Donc le coefficient directeur de la tangente en
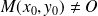 est du signe de
est du signe de
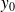 .
.
La courbe « monte » quand
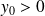 et « descend » quand
et « descend » quand
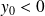 .
.
Fondamental :
Théorème des fonctions implicites
Soit
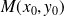 un point régulier de
un point régulier de
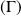 .
.
Si
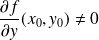 , il existe deux intervalles ouverts
, il existe deux intervalles ouverts
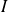 et
et
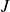 centrés en
centrés en
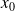 et
et
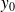 tels que
tels que
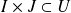 , et une fonction
, et une fonction
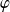 de classe
de classe
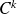 de
de
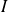 dans
dans
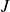 telle que :
telle que :
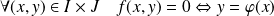 . Alors :
. Alors :
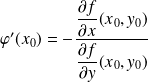 .
.Si
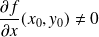 , il existe deux intervalles ouverts
, il existe deux intervalles ouverts
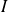 et
et
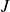 centrés en
centrés en
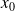 et
et
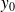 tels que
tels que
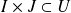 , et une fonction
, et une fonction
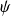 de classe
de classe
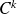 de
de
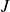 dans
dans
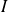 telle que :
telle que :
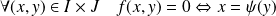 . Alors :
. Alors :
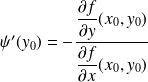 .
.
Si
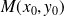 est un point régulier de
est un point régulier de
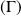 , on peut exprimer localement
, on peut exprimer localement
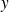 en fonction de
en fonction de
 , ou
, ou
 en fonction de
en fonction de
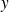 .
.
Si
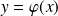 , la tangente à
, la tangente à
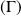 en
en
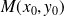 a pour coefficient directeur
a pour coefficient directeur
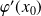 .
.
Et si
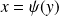 , la tangente à
, la tangente à
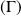 en
en
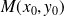 a pour coefficient directeur
a pour coefficient directeur
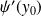 .
.
Méthode :
Etude en un point stationnaire
Pour obtenir la tangente, il faut étudier la limite de
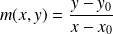 lorsque le point
lorsque le point
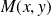 tend sur la courbe vers le point
tend sur la courbe vers le point
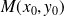 .
.
Il faut donc que
 tende vers
tende vers
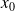 et que
et que
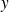 tende vers
tende vers
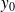 avec
avec
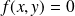 .
.
Dans l'exemple précédent, il s'agit d'étudier l'existence d'une tangente au point
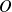 .
.
Pour tout
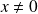 , on pose
, on pose
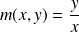 , donc :
, donc :
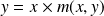 . Donc l'équation peut s'écrire :
. Donc l'équation peut s'écrire :
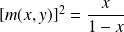 car
car
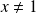 .
.
Donc si
 tend vers
tend vers
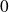 , alors
, alors
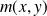 tend vers
tend vers
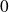 .
.
Donc la tangente au point
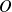 à la courbe
à la courbe
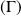 est horizontale.
est horizontale.
Méthode :
Etude des branches infinies
En s'aidant de la localisation de la courbe, on peut voir si
 ou
ou
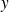 peuvent tendre vers l'infini.
peuvent tendre vers l'infini.Suivant les cas, on étudie l'intersection de la courbe avec des droites horizontales ou verticales ou d'équation
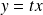 .
.
Dans l'exemple précédent, on a vu que la courbe
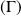 est incluse dans la partie de plan :
est incluse dans la partie de plan :
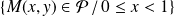 .
.
Donc, sur la courbe,
 ne peut pas tendre vers l'infini. Donc il ne peut y avoir une branche infinie que si
ne peut pas tendre vers l'infini. Donc il ne peut y avoir une branche infinie que si
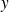 tend vers l'infini.
tend vers l'infini.
Donc cela ne peut correspondre qu'à une asymptote verticale.