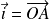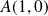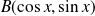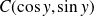Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Déterminer les triangles d'aire maximale inscrits dans un cercle donné.
Utilisez un paramétrage du cercle pour vous ramener à la recherche du maximum d'une fonction de
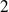variables.
Par homothétie, on peut se ramener à un cercle de rayon
Soit
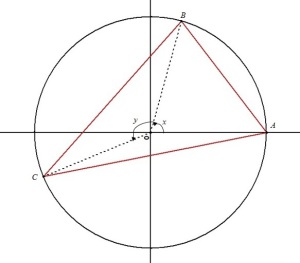
On choisit un repère orthonormé d'origine
Dans ce repère, les coordonnées des points sont : où les réels
|  |
L'aire du triangle est :
.
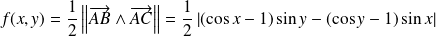Or :
.
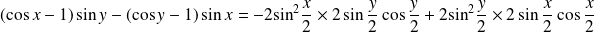Donc :
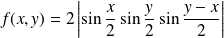. Or :
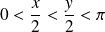, donc :
.
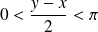Donc :
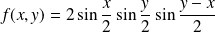avec
.
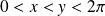Il s'agit de trouver le maximum de cette fonction sur l'ouvert
.
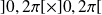La fonction
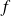est de classe
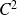sur l'ouvert
.
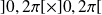Ses dérivées partielles d'ordre
sont :
.
.
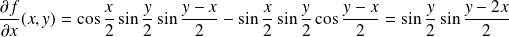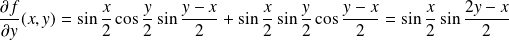Or :
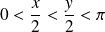, donc :
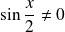, et :
.
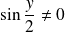Donc les points critiques sont solutions du système :
.
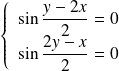Or :
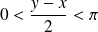, et :
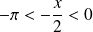. Donc :
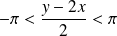, et :
.
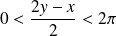Donc les points critiques sont solutions du système :
.
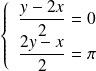Donc la fonction
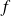admet un seul point critique :
.
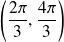Ses dérivées partielles d'ordre
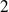sont :
.
.
.
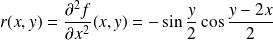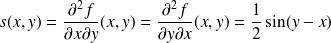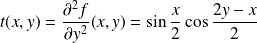Donc :
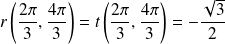, et :
.
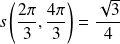Donc, au point
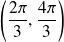, on a :
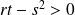et
.
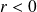Donc, sur
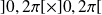, la fonction
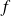admet un maximum local en
.
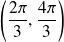Ce maximum correspond à un triangle équilatéral et :
.
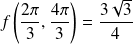Or la fonction
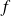est continue sur le compact
.
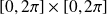Il existe donc un maximum absolu de
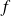sur ce compact. Il est atteint soit sur l'intérieur
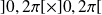, soit sur la frontière.
Or :
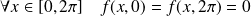, et :
.
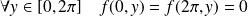Donc le maximum n'est pas atteint sur la frontière.
Donc le maximum local en
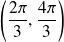est un maximum global.
Conclusion : Les triangles d'aire maximale inscrits dans un cercle donné sont les triangles équilatéraux.
