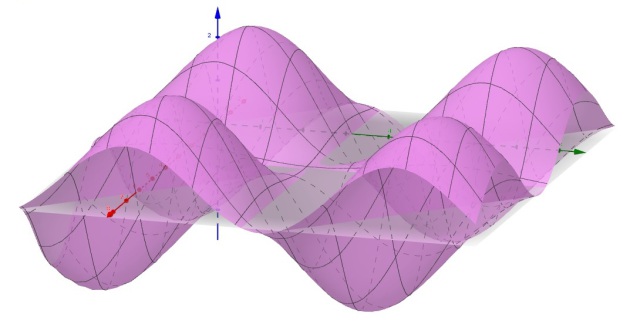
Extremums d'une fonction numérique
Soit
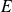 un espace vectoriel normé de base orthonormale
un espace vectoriel normé de base orthonormale
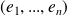 .
.
Les fonctions utilisées sont définies sur un ouvert
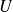 non vide de
non vide de
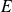 à valeurs dans
à valeurs dans
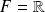 .
.
Définition :
Si
 est de classe
est de classe
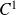 sur l'ouvert
sur l'ouvert
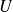 , le gradient de
, le gradient de
 en un point
en un point
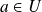 est le vecteur de coordonnées :
est le vecteur de coordonnées :
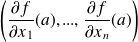 .
.
Il est noté
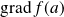 ou
ou
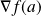 .
.
Par exemple, si
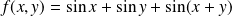 , alors :
, alors :
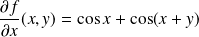 , et :
, et :
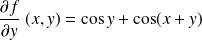 .
.
Donc :
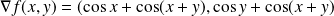 . Donc par exemple :
. Donc par exemple :
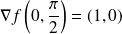 .
.
Fondamental :
Propriétés
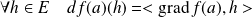 si la base
si la base
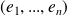 est orthonormale.
est orthonormale.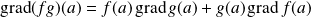 .
.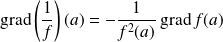 si
si
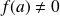 .
.
La première propriété se traduit par :
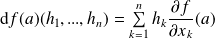 déjà vu précédemment.
déjà vu précédemment.
Définition :
Extremum
 admet un maximum local en
admet un maximum local en
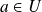 si :
si :
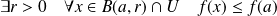 .
.C'est un maximum global si :
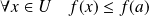 .
.
 admet un minimum local en
admet un minimum local en
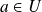 si :
si :
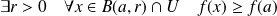 .
.C'est un minimum global si :
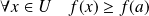 .
.
Fondamental :
Condition nécessaire d'extremum local
Si la fonction
 de classe
de classe
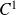 sur un ouvert
sur un ouvert
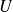 admet un extremum local en
admet un extremum local en
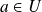 , alors
, alors
 est un point critique :
est un point critique :
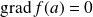 .
.
Donc les extremums de
 sont à chercher parmi les points qui vérifient :
sont à chercher parmi les points qui vérifient :
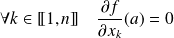 .
.
Dans l'exemple précédent, les points critiques sont solutions du système :
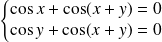 .
.
Or :
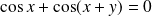 si et seulement si :
si et seulement si :
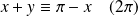 ou
ou
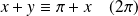 .
.
Et :
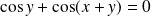 si et seulement si :
si et seulement si :
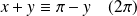 ou
ou
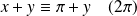 .
.
Sur l'ouvert
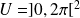 , on obtient trois points critiques :
, on obtient trois points critiques :
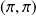 ,
,
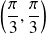 et
et
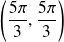 .
.
Définition :
Cas d'une fonction de 2 variables
Si la fonction
 est de classe
est de classe
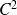 sur un ouvert
sur un ouvert
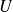 non vide de
non vide de
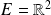 , on note usuellement :
, on note usuellement :
ses dérivées partielles d'ordre
 :
:
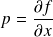 et
et
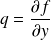
ses dérivées partielles d'ordre
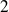 :
:
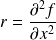 ,
,
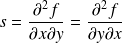 et
et
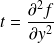 .
.
Ces notations s'appellent les notations de Monge.
Dans l'exemple précédent, les dérivées partielles d'ordre
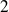 sont :
sont :
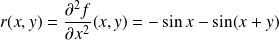 .
.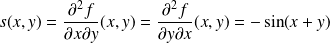 .
.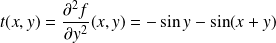 .
.
Fondamental :
Développement limité d'ordre 2
Si
 est de classe
est de classe
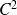 sur un ouvert
sur un ouvert
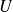 non vide de
non vide de
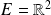 et si
et si
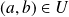 , alors
, alors
 admet un développement limité d'ordre
admet un développement limité d'ordre
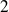 .
.
Il existe un réel
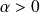 tel que pour tout
tel que pour tout
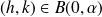 :
:
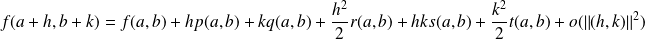 .
.
Donc si
 est un point critique :
est un point critique :
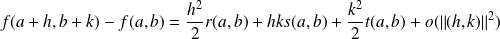 .
.
Fondamental :
Existence d'un extremum local en un point critique
Si
 est de classe
est de classe
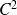 sur un ouvert
sur un ouvert
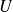 non vide de
non vide de
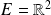 et si
et si
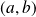 est un point critique (
est un point critique (
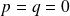 ) :
) :
Si
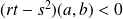 : la fonction
: la fonction
 n'admet pas d'extremum en
n'admet pas d'extremum en
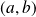 : c'est un point col (ou point selle).
: c'est un point col (ou point selle).Si
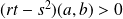 et
et
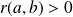 : la fonction
: la fonction
 admet un minimum local en
admet un minimum local en
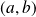 .
.Si
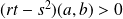 et
et
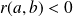 : la fonction
: la fonction
 admet un maximum local en
admet un maximum local en
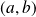 .
.Si
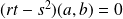 , on ne peut pas conclure.
, on ne peut pas conclure.
Dans l'exemple précédent :
au point
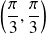 , on a :
, on a :
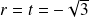 et
et
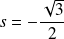 , donc :
, donc :
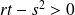 et
et
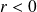 .
.Donc la fonction
 admet un maximum local au point
admet un maximum local au point
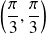 .
.au point
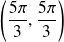 , on a :
, on a :
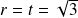 et
et
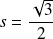 , donc :
, donc :
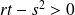 et
et
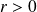 .
.Donc la fonction
 admet un minimum local au point
admet un minimum local au point
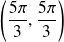 .
.au point
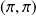 , on a :
, on a :
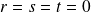 , donc :
, donc :
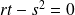 . On ne peut pas conclure par cette méthode.
. On ne peut pas conclure par cette méthode.On a :
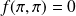 et pour tout
et pour tout
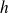 :
:
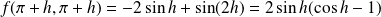 est du signe contraire de
est du signe contraire de
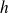 .
.Donc
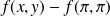 ne garde pas un signe constant au voisinage de
ne garde pas un signe constant au voisinage de
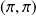 .
.Donc la fonction
 n'admet ni maximum local, ni minimum local au point
n'admet ni maximum local, ni minimum local au point
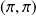 : c'est un point col.
: c'est un point col.
Méthode :
Existence d'un extremum global
Un extremum global est à chercher parmi les extrema locaux en étudiant le signe de
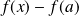 .
.
Rappel : Si
 est continue sur un compact, elle est bornée, donc admet un maximum global et un minimum global.
est continue sur un compact, elle est bornée, donc admet un maximum global et un minimum global.
Fondamental :
Cas d'une fonction de n variables
Si la fonction
 est de classe
est de classe
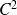 sur un ouvert
sur un ouvert
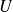 de
de
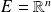 et si
et si
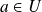 , alors il existe
, alors il existe
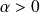 tel que pour tout
tel que pour tout
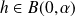 :
:
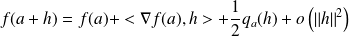 avec
avec
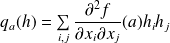 .
.
Si la fonction
 est de classe
est de classe
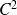 sur un ouvert
sur un ouvert
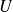 de
de
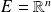 , alors pour tout point critique
, alors pour tout point critique
 :
:
Si
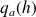 est strictement négatif pour tout
est strictement négatif pour tout
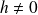 , alors
, alors
 admet un maximum local en
admet un maximum local en
 .
.Si
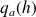 est strictement positif pour tout
est strictement positif pour tout
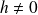 , alors
, alors
 admet un minimum local en
admet un minimum local en
 .
.S'il existe des vecteurs
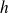 et
et
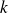 tels que
tels que
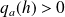 et
et
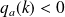 , alors
, alors
 n'admet pas d'extremum en
n'admet pas d'extremum en
 .
.