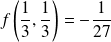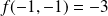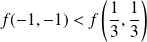Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
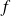 la fonction définie par :
la fonction définie par :
 .
.
Question
Déterminer, s'ils existent, les points critiques de la fonction
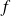 .
.
Les points critiques annulent les dérivées partielles de
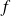 .
.
La fonction
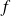 est polynômiale, donc de classe
est polynômiale, donc de classe
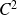 sur l'ouvert
sur l'ouvert
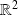 .
.
Ses dérivées partielles d'ordre
 sont :
sont :
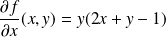 .
.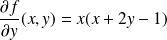 .
.
Les points critiques de
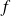 sont solutions de :
sont solutions de :
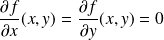 .
.
On obtient le système :
 , donc :
, donc :
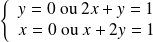 .
.
Donc :
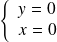 ou
ou
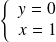 ou
ou
 ou
ou
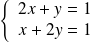 .
.
Conclusion : La fonction
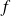 admet quatre points critiques
admet quatre points critiques
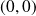 ,
,
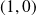 ,
,
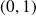 et
et
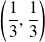 .
.
Question
Déterminer, s'ils existent, les extremums locaux de la fonction
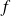 .
.
Pour chaque point critique, calculez
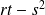 (notations de Monge).
(notations de Monge).
Les extremums locaux de la fonction
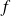 sont à chercher parmi les points critiques.
sont à chercher parmi les points critiques.
Les dérivées partielles d'ordre
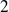 de
de
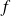 sont :
sont :
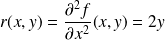 .
.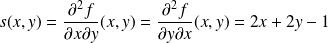 .
. .
.
Au point
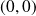 , on a :
, on a :
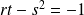 , donc :
, donc :
 , donc il n'y a pas d'extremum local.
, donc il n'y a pas d'extremum local.
Au point
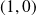 , on a :
, on a :
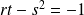 , donc :
, donc :
 , donc il n'y a pas d'extremum local.
, donc il n'y a pas d'extremum local.
Au point
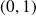 , on a :
, on a :
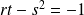 , donc :
, donc :
 , donc il n'y a pas d'extremum local.
, donc il n'y a pas d'extremum local.
Au point
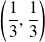 , on a :
, on a :
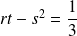 et
et
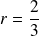 , donc
, donc
 .
.
Conclusion : La fonction
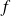 admet un minimum local au point
admet un minimum local au point
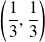 .
.
Les points
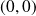 ,
,
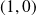 et
et
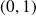 sont des points cols.
sont des points cols.