Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Les deux questions sont indépendantes.
Question
Déterminer les fonctions à valeurs réelles solutions du système :
.
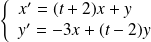Diagonalisez la matrice
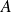du système :
.
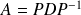Puis déterminez les fonctions
et
telles que :
.
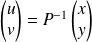Il s'agit d'un système différentiel linéaire à coefficients non constants.
Le système équivaut à l'équation :
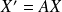avec :
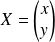et
.
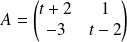Le polynôme caractéristique de
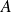est :
.
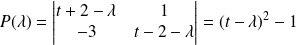Donc la matrice
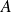admet deux valeurs propres distinctes :
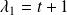et
.
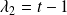Le sous espace propre associé à
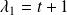est la droite vectorielle de base :
.
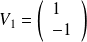Le sous espace propre associé à
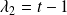est la droite vectorielle de base :
.
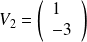Donc
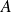est diagonalisable :
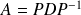avec :
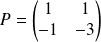et
.
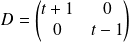L'équation
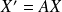équivaut à :
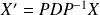, donc à :
.
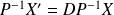La matrice
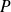ne dépend pas de la variable
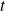, donc si
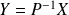, alors :
.
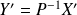Donc l'équation équivaut à :
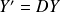, donc à :
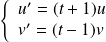en posant :
.
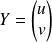Donc il existe
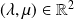tel que :
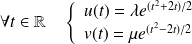. Or :
.
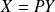Conclusion :
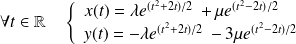où
.
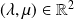Question
Déterminer les fonctions à valeurs réelles solutions du système :
.
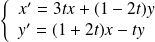Diagonalisez la matrice
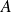du système :
.
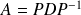Puis déterminez les fonctions
et
telles que :
.
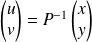Il s'agit aussi d'un système différentiel linéaire à coefficients non constants.
Le système équivaut à l'équation
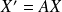avec :
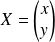et
.
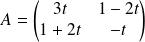Le polynôme caractéristique de
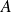est :
.
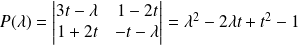Donc la matrice
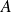admet deux valeurs propres distinctes :
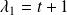et
.
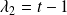Le sous espace propre associé à
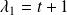est la droite vectorielle de base :
.
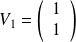Le sous espace propre associé à
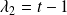est la droite vectorielle de base :
.
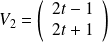Donc
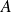est diagonalisable :
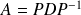avec :
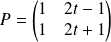et
.
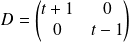L'équation
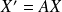équivaut à :
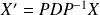, donc à :
.
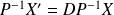Mais ici la matrice
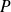dépend de la variable
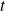, donc si
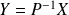, alors :
.
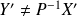On pose :
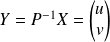, donc :
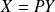, donc :
.
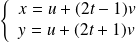Donc :
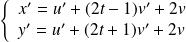, donc :
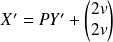, donc :
.
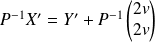Or :
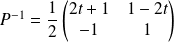. Donc :
.
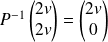Donc l'équation
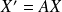équivaut à :
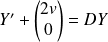, donc à :
.
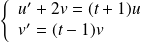On résout la deuxième équation. Il existe
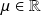tel que :
.
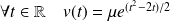La première équation devient :
.
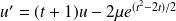L'équation homogène associée a pour solutions :
.
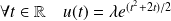On utilise la méthode de variation de la constante :
.
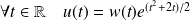La fonction
est solution si :
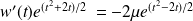, donc si :
.
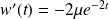Donc il existe
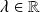tel que :
.
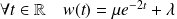Donc :
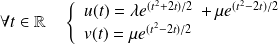où
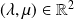. Or :
.
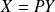Conclusion :
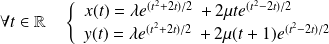où
.
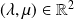