Exo 11
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le système différentiel :
.
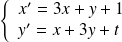Question
Déterminer les fonctions à valeurs réelles solutions de ce système.
Déterminez les valeurs propres et les vecteurs propres de la matrice du système homogène pour le résoudre.
Ensuite, utilisez la méthode de variation de constante.
Il s'agit d'un système différentiel linéaire à coefficients constants.
Le système s'écrit matriciellement :
.
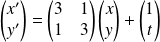Le polynôme caractéristique de
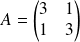est :
.
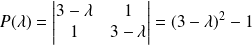La matrice
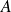est donc diagonalisable car elle a deux valeurs propres distinctes
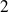et
.
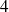A la valeur propre
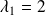correspond un vecteur propre
.
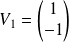A la valeur propre
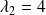correspond un vecteur propre
.
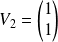Donc les fonctions définies par :
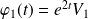et
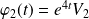forment un système fondamental de solutions du système différentiel homogène.
Pour résoudre le système proposé, on utilise la méthode de variation de constante.
Une fonction définie par :
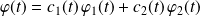est solution du système si et seulement si :
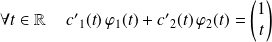, donc si :
.
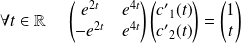La matrice
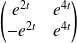a pour déterminant
(
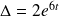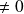), donc est inversible.
Donc
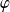est solution si et seulement si :
.
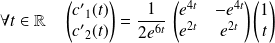Donc :
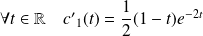et :
.
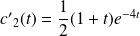On détermine les fonctions
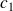et
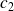en intégrant par parties.
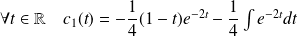, donc :
.
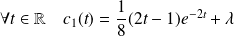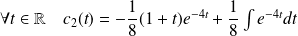, donc :
.
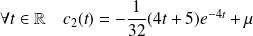Donc :
.
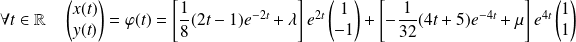Conclusion :
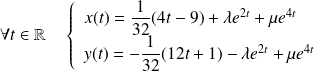où
.
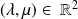