Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère le système différentiel :
.
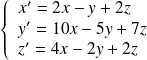Question
Déterminer les fonctions à valeurs réelles solutions de ce système.
Réduisez la matrice
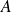du système pour déterminer la matrice
.
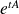Il s'agit d'un système différentiel linéaire à coefficients constants et homogène.
Le système s'écrit matriciellement :
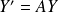avec
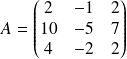et
.
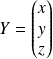Les solutions sont les fonctions :
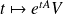où
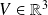et
.
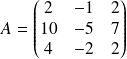Pour calculer la matrice
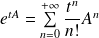, on va réduire la matrice
.
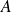Son polynôme caractéristique est :
.
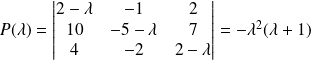La matrice
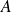n'a donc que deux valeurs propres :
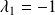et
.
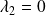Le sous-espace propre associé à
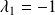est la droite vectorielle de base
.
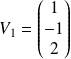Le sous-espace propre associé à
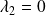est la droite vectorielle de base
.
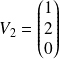Donc la matrice
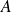n'est pas diagonalisable. On cherche donc à la trianguler.
Si
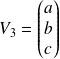, alors :
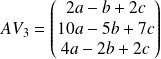. La troisième coordonnée est nulle si :
.
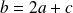Alors
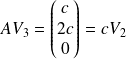. On choisit
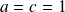, donc :
.
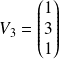Les vecteurs
,
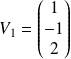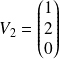et
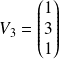forment une base
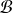de
.
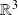La matrice de passage de la base canonique à la base
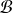est :
.
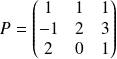Son inverse est :
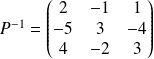, et :
.
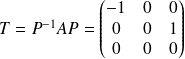Donc :
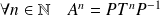, donc :
.
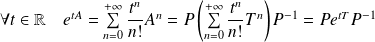Il s'agit donc de calculer les puissances de la matrice
.
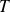Les premiers termes donnent :
,
, ...
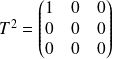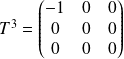Une simple récurrence montre que :
.
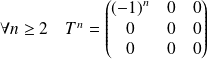Donc :
.
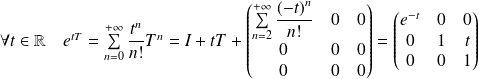Donc :
.
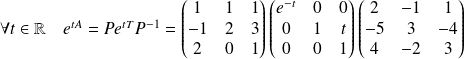Donc :
.
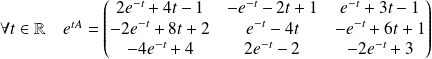Les solutions de l'équation
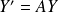sont les fonctions :
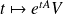où
.
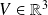Conclusion :
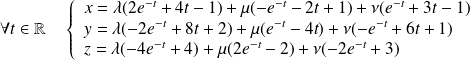où
.
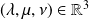