Autres équations différentielles linéaires
Définition :
Une équation différentielle linéaire scalaire d'ordre p est une équation de la forme :
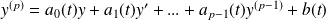 où
où
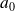 , ...,
, ...,
 et
et
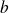 sont des fonctions continues sur
sont des fonctions continues sur
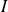 à valeurs dans
à valeurs dans
 ou
ou
 .
.
On peut remarquer que l'équation équivaut à :
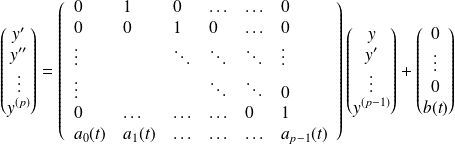 .
.
Donc, si l'on pose :
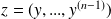 , on obtient une équation de la forme :
, on obtient une équation de la forme :
 où
où
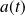 est une application linéaire de
est une application linéaire de
 dans
dans
 et
et
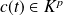 . On se ramène ainsi à une équation différentielle du premier ordre.
. On se ramène ainsi à une équation différentielle du premier ordre.
Plus généralement, dans la suite, les fonctions considérées sont définies sur un intervalle
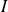 de
de
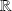 et à valeurs dans un espace vectoriel normé
et à valeurs dans un espace vectoriel normé
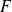 de dimension finie
de dimension finie
 .
.
Définition :
On appelle équation différentielle linéaire du premier ordre toute équation
 de la forme :
de la forme :
 , où
, où
 est une fonction continue de
est une fonction continue de
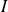 dans
dans
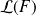 , et
, et
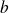 une fonction continue de
une fonction continue de
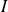 dans
dans
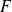 .
.
L'équation homogène associée
 est l'équation :
est l'équation :
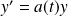 .
.
Une fonction
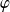 de
de
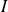 dans
dans
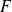 est solution de
est solution de
 si
si
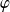 est dérivable sur
est dérivable sur
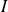 et si :
et si :
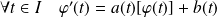 .
.
Dans l'équation
 , la notation
, la notation
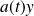 signifie
signifie
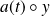 .
.
Et
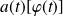 appartient à
appartient à
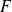 puisque
puisque
 appartient à
appartient à
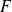 et que
et que
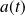 est une application linéaire de
est une application linéaire de
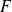 dans
dans
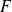 .
.
Fondamental :
Propriétés
Soit
 l'équation différentielle
l'équation différentielle
 ,
,
 l'équation homogène associée, et soit
l'équation homogène associée, et soit
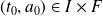 .
.
Toute solution de l'équation différentielle
 est de classe
est de classe
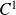 sur
sur
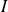 .
.Théorème de Cauchy-Lipschitz : Il existe une unique solution
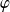 de l'équation
de l'équation
 qui vérifie la condition initiale
qui vérifie la condition initiale
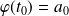 .
.L'ensemble
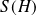 des solutions de
des solutions de
 est un sous-espace vectoriel de
est un sous-espace vectoriel de
 isomorphe à
isomorphe à
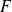 .
.Si
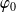 est une solution particulière de
est une solution particulière de
 , une fonction
, une fonction
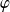 est solution de
est solution de
 si et seulement si
si et seulement si
 est solution de
est solution de
 .
.
Pour tout
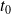 de
de
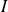 , l'application
, l'application
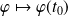 est un isomorphisme entre
est un isomorphisme entre
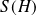 et
et
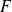 . Donc :
. Donc :
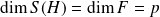 .
.
Définition :
Un système fondamental de solutions de
 est constitué de
est constitué de
 solutions de
solutions de
 linéairement indépendantes.
linéairement indépendantes.
Soit
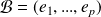 une base de
une base de
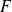 . Pour tout
. Pour tout
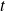 de
de
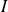 , on note
, on note
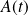 la matrice de l'application linéaire
la matrice de l'application linéaire
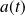 dans cette base et
dans cette base et
 celle de
celle de
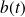 .
.
A toute fonction
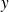 dérivable sur
dérivable sur
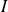 , on associe ses fonctions coordonnées
, on associe ses fonctions coordonnées
 , ...,
, ...,
 , et leurs dérivées.
, et leurs dérivées.
L'équation différentielle peut donc s'écrire sous forme matricielle :
 où
où
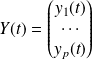 .
.
Elle peut aussi se traduire par le système différentiel :
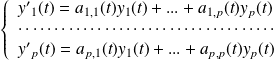 .
.
Réciproquement, tout système différentiel de cette forme peut s'écrire sous la forme :
 .
.
Fondamental :
Soit
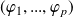 est une famille de
est une famille de
 éléments de
éléments de
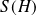 . Pour tout
. Pour tout
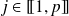 , on note :
, on note :
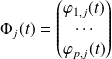 si
si
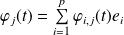 .
.
On appelle wronskien de
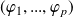 le déterminant :
le déterminant :
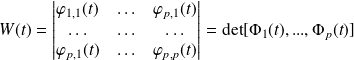 .
.
La famille
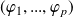 est un système fondamental de solutions de
est un système fondamental de solutions de
 si et seulement si il existe
si et seulement si il existe
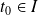 tel que
tel que
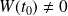 .
.
Si
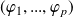 est un système fondamental de solutions de
est un système fondamental de solutions de
 , alors
, alors
 pour tout
pour tout
 .
.
Fondamental :
Cas où les coefficients sont constants
L'équation
 est à coefficients constants si l'application
est à coefficients constants si l'application
 est constante : son image (notée
est constante : son image (notée
 ) est un endomorphisme de
) est un endomorphisme de
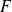 .
.
Les solutions de l'équation différentielle homogène
 sont les fonctions
sont les fonctions
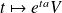 où
où
 .
.
Si l'endomorphisme
 est diagonalisable et si
est diagonalisable et si
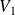 , ...,
, ...,
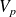 forment une base de vecteurs propres associés aux valeurs propres
forment une base de vecteurs propres associés aux valeurs propres
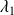 , ...,
, ...,
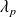 , alors les
, alors les
 fonctions définies par
fonctions définies par
 forment un système fondamental de solutions de
forment un système fondamental de solutions de
 .
.
Rappel :
 est un endomorphisme de
est un endomorphisme de
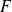 .
.
Si
 est un vecteur propre associé à la valeur propre
est un vecteur propre associé à la valeur propre
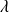 , alors :
, alors :
 .
.
Méthode :
Méthode de variation de constante
Soit
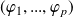 un système fondamental de solutions de
un système fondamental de solutions de
 .
.
Si
 , ...,
, ...,
 sont des fonctions de classe
sont des fonctions de classe
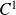 sur
sur
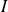 , la fonction définie par :
, la fonction définie par :
 est solution de l'équation
est solution de l'équation
 si et seulement si :
si et seulement si :
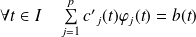 .
.
Cette égalité aboutit à un système de Cramer qui permet de déterminer les dérivées
 , puis les fonctions
, puis les fonctions
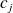 .
.
Fondamental :
Cas d'une équation linéaire scalaire homogène d'ordre p à coefficients constants :
 .
.
On lui associe son équation caractéristique :
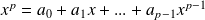 .
.
L'ensemble des solutions est un espace vectoriel de dimension
 .
.La fonction
 est solution de
est solution de
 si et seulement si
si et seulement si
 est racine de l'équation caractéristique.
est racine de l'équation caractéristique.Si
 est racine d'ordre
est racine d'ordre
 de l'équation caractéristique, toutes les fonctions
de l'équation caractéristique, toutes les fonctions
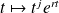 avec
avec
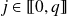 sont solutions de
sont solutions de
 .
.





