Exo 4
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
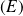l'équation différentielle :
.
Question
Montrer que
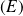admet une solution de la forme
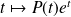où
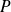est un polynôme.
Commencez par déterminer le degré du polynôme.
Soit
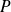un polynôme et
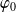la fonction définie par :
.
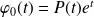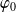est solution de
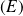si :
.
Donc :
.
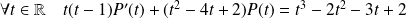Comme
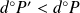, le degré du premier membre est
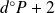. Donc, il faut que :
.
Donc
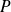est de la forme :
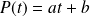, et :
.
Donc :
.
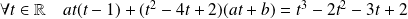Par identification, on obtient :
.
Conclusion : La fonction
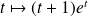est solution de l'équation
.
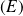Question
Résoudre l'équation
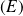sur les intervalles
,
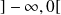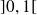et
.
Résolvez l'équation homogène associée.
L'équation
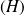homogène associée à
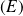est :
.
Sur chaque intervalle, elle équivaut à :
.
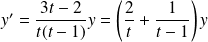Une primitive de la fonction
est :
.
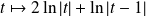Donc les solutions de
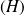sont de la forme :
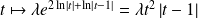avec
.
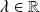Or la fonction
a un signe constant sur chaque intervalle.
Donc, sur chacun des intervalles, les solutions de
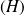sont de la forme :
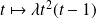avec
.
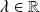Conclusion : Sur chacun des intervalles, les solutions de
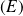sont les fonctions de la forme
avec
.
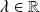Question
Résoudre l'équation différentielle
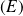sur
.
Les solutions de
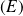sur
doivent être continues et dérivables sur
.
Si
est une solution de l'équation
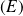sur
, sa restriction à chacun des intervalles est solution de
.
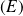Donc il existe trois réels
,
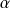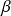et
tels que :
.
Or la fonction
doit être continue et dérivable sur
, donc en
et en
.
Or :
. Donc, il faut que :
.
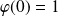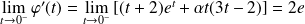et :
.
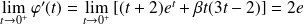Donc, en posant
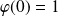, la fonction
est continue et dérivable en
pour tout
.
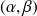Et :
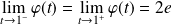. Donc, il faut que :
.
et :
.
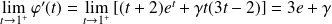Donc, en posant
, la fonction
est continue et dérivable en
si
.
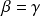Conclusion : Les solutions de
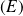sur
sont les fonctions
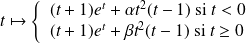avec
.
