Equations différentielles linéaires scalaires du premier ordre
Les fonctions considérées sont des fonctions définies sur un intervalle
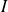 de
de
 et à valeurs dans
et à valeurs dans
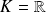 ou
ou
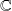 .
.
Définition :
On appelle équation différentielle linéaire scalaire du premier ordre toute équation
 de la forme :
de la forme :
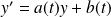 , où
, où
 et
et
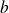 sont des fonctions continues sur
sont des fonctions continues sur
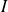 .
.
Par exemple, l'équation :
 est une équation différentielle linéaire scalaire du premier ordre.
est une équation différentielle linéaire scalaire du premier ordre.
Fondamental :
Propriétés
Soit
 l'équation différentielle
l'équation différentielle
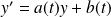 , où
, où
 et
et
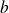 sont des fonctions continues sur
sont des fonctions continues sur
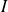 et soit
et soit
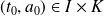 .
.
Toute solution de l'équation différentielle
 est de classe
est de classe
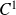 sur
sur
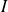 .
.Théorème de Cauchy-Lipschitz : Il existe une unique solution
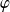 de l'équation
de l'équation
 qui vérifie la condition initiale
qui vérifie la condition initiale
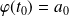 .
.
Définition :
Soit
 l'équation différentielle :
l'équation différentielle :
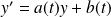 , où
, où
 et
et
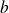 sont des fonctions continues sur
sont des fonctions continues sur
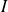 .
.
On appelle équation homogène associée à
 l'équation
l'équation
 :
:
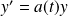 .
.
On l'appelle aussi équation sans second membre car elle peut s'écrire :
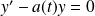 .
.
Par exemple, l'équation homogène associée à l'équation
 :
:
 est l'équation
est l'équation
 :
:
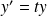 .
.
Fondamental :
Propriétés
Soit
 l'équation différentielle
l'équation différentielle
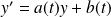 , et
, et
 l'équation homogène associée.
l'équation homogène associée.
L'ensemble
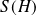 des solutions de l'équation homogène est un espace vectoriel de dimension
des solutions de l'équation homogène est un espace vectoriel de dimension
 , de base
, de base
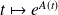 où
où
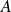 est une primitive de la fonction
est une primitive de la fonction
 sur l'intervalle
sur l'intervalle
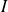 .
.Si
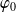 est une solution de l'équation
est une solution de l'équation
 , une fonction
, une fonction
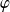 est solution de
est solution de
 si et seulement si
si et seulement si
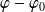 appartient à
appartient à
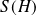 .
.
Par exemple toutes les solutions de l'équation
 :
:
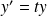 sont de la forme :
sont de la forme :
 où
où
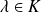 .
.
Et l'on peut remarquer que la fonction :
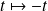 est solution de l'équation
est solution de l'équation
 :
:
 .
.
Donc l'ensemble des solutions de
 est l'ensemble des fonctions :
est l'ensemble des fonctions :
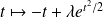 où
où
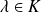 .
.
Et l'unique solution de
 qui vérifie la condition initiale
qui vérifie la condition initiale
 est la fonction :
est la fonction :
 .
.
Méthode :
Donc pour résoudre l'équation différentielle linéaire scalaire
 :
:
On détermine une primitive
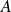 de la fonction
de la fonction
 .
.On en déduit la solution générale de l'équation homogène associée :
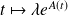 où
où
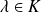 .
.On détermine une solution particulière
 de l'équation
de l'équation
 .
.On en déduit l'ensemble des solutions de
 sous la forme :
sous la forme :
 où
où
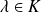 .
.
En général, l'étape la plus difficile est la détermination d'une solution particulière de
 .
.
Une autre technique est celle de la variation de constante.
Méthode :
Méthode de variation de constante
Soit
 l'équation différentielle
l'équation différentielle
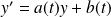 , et
, et
 l'équation homogène associée.
l'équation homogène associée.
On détermine une primitive
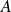 de la fonction
de la fonction
 .
.On en déduit la solution générale de l'équation homogène associée :
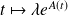 où
où
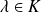 .
.On cherche une solution de l'équation
 sous la forme :
sous la forme :
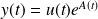 (ce qui revient à faire varier
(ce qui revient à faire varier
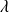 ).
).On en déduit l'expression de
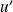 et il suffit de trouver une primitive de cette fonction pour avoir toutes les solutions de
et il suffit de trouver une primitive de cette fonction pour avoir toutes les solutions de
 .
.
Dans l'exemple précédent (en supposant que l'on n'a pas trouvé de solution particulière), on pose :
 .
.
On obtient :
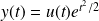 , donc :
, donc :
 .
.
Donc
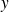 vérifie l'équation différentielle
vérifie l'équation différentielle
 si et seulement si :
si et seulement si :
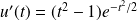 , donc si :
, donc si :
 avec
avec
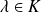 .
.
Et l'on retrouve l'expression des solutions trouvées précédemment :
 avec
avec
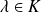 .
.





