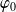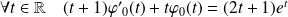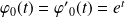Exo 3
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
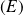l'équation différentielle :
.
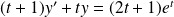Question
Question
En déduire l'ensemble des solutions de
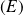sur
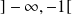et sur
.
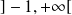Résolvez l'équation homogène et utilisez la structure de l'ensemble des solutions.
L'équation homogène associée est :
.
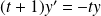Sur
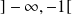et sur
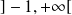, elle équivaut à :
.
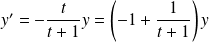Elle admet donc pour solutions les fonctions de la forme :
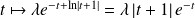où
.
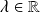Or le signe de
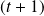est constant sur chacun des deux intervalles.
Donc, en changeant éventuellement le signe de
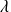, elles sont de la forme :
.
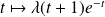Conclusion : Les solutions de
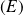sur
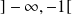et sur
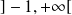sont les fonctions
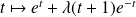où
.
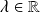Question
En déduire l'ensemble des solutions de
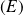sur
.
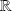Les solutions doivent être continues et dérivables sur
.
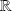Soit
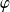une solution de
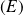sur
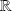. Donc :
.
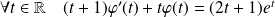Donc :
.
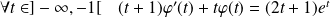Donc la restriction de
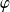à
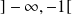est solution de
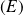sur
.
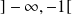Donc il existe un réel
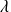tel que :
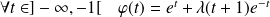. Et :
.
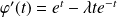Donc :
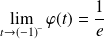et
.
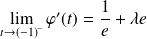De même la restriction de
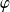à
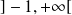est solution de
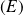sur
.
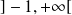Donc il existe un réel
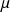tel que :
.
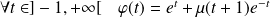Donc :
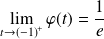et
.
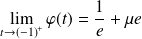Or la fonction
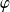est continue et dérivable sur
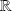, donc en
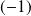. Donc :
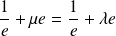. Donc :
.
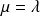Conclusion : Les solutions de
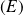sur
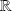sont les fonctions
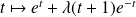où
.
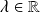