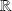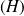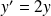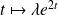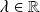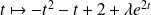Exo 1
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
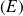 l'équation différentielle :
l'équation différentielle :
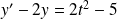 .
.
Question
Montrer que l'équation
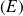 admet une unique solution polynômiale.
admet une unique solution polynômiale.
Commencez par déterminer le degré du polynôme.
Une fonction
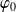 est solution de
est solution de
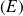 si :
si :
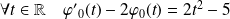 .
.
Si
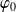 est polynômiale, alors :
est polynômiale, alors :
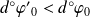 . Donc :
. Donc :
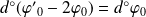 .
.
Donc il faut que :
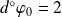 . Donc
. Donc
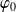 est de la forme :
est de la forme :
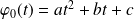 .
.
Donc :
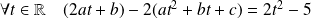 .
.
Donc :
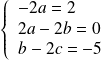 . Donc :
. Donc :
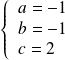 .
.
Conclusion : La fonction
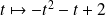 est l'unique solution polynômiale de l'équation
est l'unique solution polynômiale de l'équation
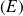 .
.
Question
Question
Déterminer la solution
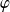 de
de
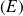 qui vérifie la condition initiale :
qui vérifie la condition initiale :
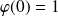 .
.
La fonction
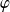 cherchée est de la forme :
cherchée est de la forme :
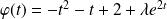 , donc :
, donc :
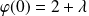 .
.
Donc :
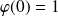 si et seulement si :
si et seulement si :
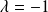 .
.
Conclusion :
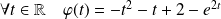 .
.