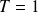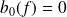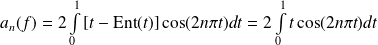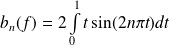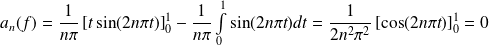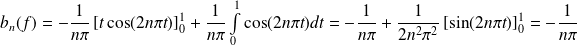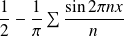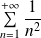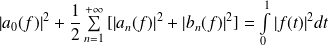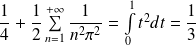Exo 15
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
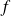la fonction définie par :
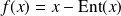où
est la partie entière de
.
Question
Question
Etudier la convergence de cette série de Fourier et en déduire la somme :
.
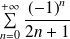Utilisez le théorème de Dirichlet, puis une valeur particulière de
.
La fonction
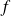est de classe
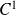par morceaux sur
.
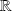Donc, d'après le théorème de Dirichlet, sa série de Fourier converge simplement vers la fonction régularisée de
.
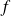Or la fonction
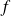est continue sur
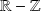. Donc :
.
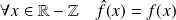Donc :
.
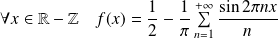Pour
:
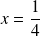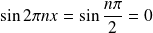si
est pair, et :
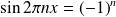si
est impair.
Donc :
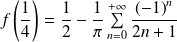. Or :
.
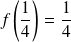Conclusion :
.
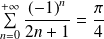