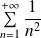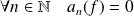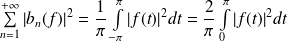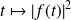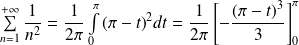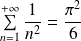Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
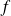la fonction impaire et
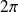- périodique définie par :
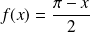si
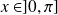et
.
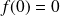Question
Montrer que la fonction
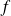est développable en série de Fourier.
Etudiez la régularisée de la fonction
.
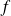La fonction
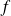est affine, donc continue et de classe
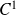sur
.
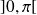De plus, la fonction
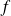est impaire et
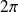- périodique.
Donc la fonction
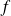est de classe
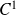par morceaux sur
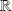, et donc, d'après le théorème de Dirichlet, sa série de Fourier converge simplement vers la fonction
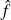régularisée de
:
.
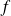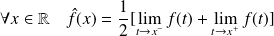La fonction
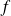est impaire, donc :
.
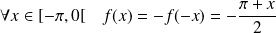Donc :
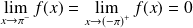. Donc
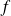est continue sur
.
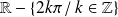De plus :
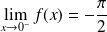et :
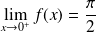. Donc :
.
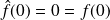Donc la fonction
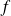est égale à sa régularisée
.
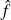Conclusion : La fonction
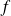est développable en série de Fourier.
Question
Déterminer le développement en série de Fourier de la fonction
.
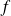Calculez les coefficients trigonométriques de
.
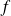La fonction
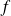est impaire. Donc :
.
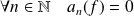Et :
.
On intègre par parties :
.
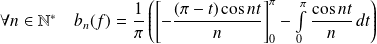Donc :
.
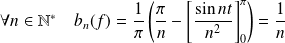Conclusion :
.
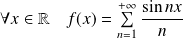Remarque :
Par exemple, pour
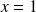, on obtient la convergence de la série
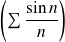et la valeur de sa somme :
.
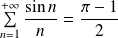