Développement d'une fonction en série de Fourier
Définition :
Soit
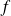une fonction continue par morceaux sur
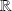et périodique de période
.
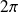Soit
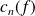les coefficients de Fourier de
,
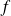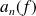et
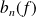les coefficients trigonométriques associés.
La série de Fourier de
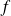est la série de fonctions définie par :
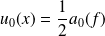et :
.
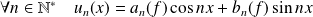Ses sommes partielles sont :
.
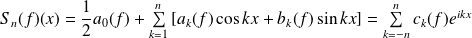Fondamental :
Propriétés
Soit
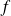une fonction définie sur
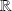et
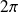-périodique.
Si
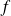est continue sur
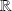, sa série de Fourier converge vers
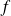en moyenne quadratique :
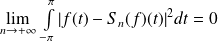
Théorème de Dirichlet : Si
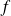est de classe
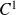par morceaux, sa série de Fourier converge simplement vers sa fonction régularisée :
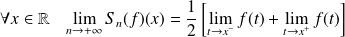.Si
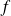est continue et de classe
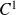par morceaux, sa série de Fourier converge normalement, donc uniformément vers
.
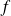Définition :
La fonction
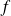est développable en série de Fourier si sa série de Fourier converge simplement vers
.
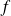Toute fonction
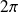-périodique, continue sur sur
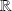et de classe
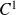par morceaux est développable en série de Fourier.
Fondamental :
Formule de Parseval
Si
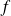est une fonction continue par morceaux et
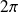-périodique :
.
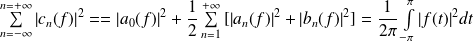Définition :
Cas des autres fonctions périodiques
Si
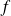est continue par morceaux et
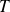-périodique, les résultats sont identiques en définissant :
.
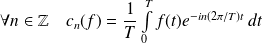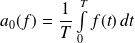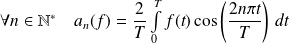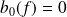et
. 
et
.
.
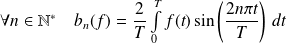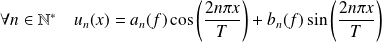Les intégrales peuvent être calculées sur n'importe quel intervalle de longueur
.
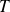La formule de Parseval devient :
.
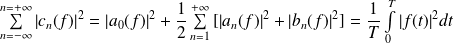