Exo 12
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
On considère la série de fonctions
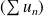définie par :
.
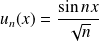Question
Démontrer que la série
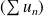converge simplement sur
.
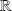Utilisez la transformation d'Abel en posant :
.
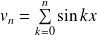Les fonctions
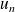sont
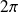- périodiques et impaires, donc il suffit d'étudier la convergence sur
.
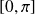En
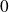, la série
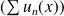est nulle, donc convergente.
On suppose donc dans la suite que :
.
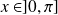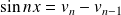en posant :
.
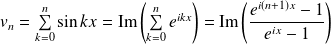Donc :
.
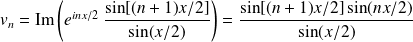Donc la suite
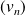est bornée car :
.
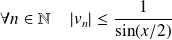Et :
.
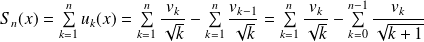Donc :
.
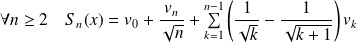Or :
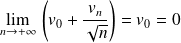car :
.
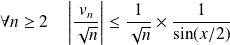Et :
.
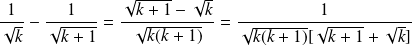Donc :
.
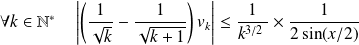Donc la série de terme général
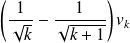est absolument convergente.
Donc la somme
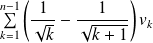a une limite finie ainsi que
.
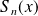Conclusion : La série
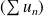converge simplement sur
.
Question
Démontrer que la série trigonométrique
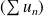n'est pas une série de Fourier.
Raisonnez par l'absurde.
Supposons que la série trigonométrique
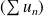soit la série de Fourier d'une fonction
.
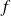Alors la fonction
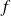serait continue par morceaux et
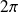- périodique.
On aurait :
.
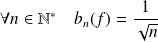Et, d'après l'inégalité de Bessel, la série
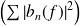serait convergente.
Or la série
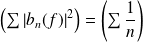diverge.
Conclusion : La série trigonométrique
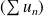n'est pas la série de Fourier d'une fonction.
Et la fonction définie par :
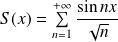n'est pas développable en série de Fourier.
