Séries de Fourier
Définition :
Une série trigonométrique est une série de fonctions de la forme :
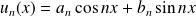où
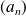et
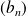sont des suites numériques.
Or :
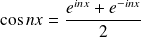et
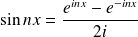, donc :
.
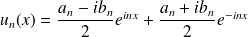Donc les sommes partielles de la série peuvent s'écrire :
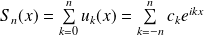en posant :
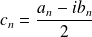et
.
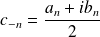Donc si la série converge, sa somme peut s'écrire :
.
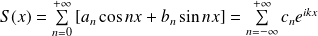Fondamental :
Propriétés de la somme d'une série trigonométrique convergente
Soit
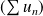une série trigonométrique convergente.
La somme
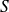est périodique de période
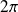.Si les séries
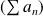et
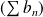sont absolument convergentes, la série converge normalement sur
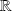et la somme
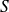est continue. Si la somme
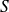est continue par morceaux, alors : 
.
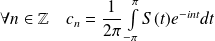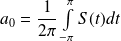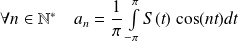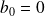et :
.
et :
.
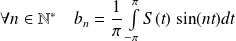Les fonctions étant périodiques de période
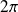, les intégrales peuvent être prises sur n'importe quel intervalle de longueur
.
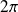Inversement, à toute fonction
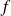continue par morceaux et périodique de période
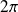, on peut associer une série trigonométrique.
Définition :
Soit
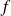une fonction continue par morceaux sur
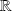, périodique de période
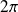et à valeurs dans
.
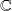On définit les coefficients de Fourier de
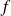par :
.
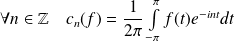Fondamental :
Propriétés
Pour tout entier
, l'application
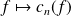est une forme linéaire.
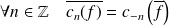. Donc si
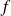est réelle :
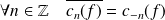.Si
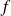est paire :
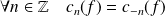. Si
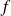est impaire :
.
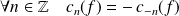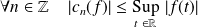.Si
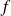est continue et de classe
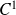par morceaux :
.
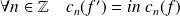On définit de même les coefficients trigonométriques et la série trigonométrique associée.
Définition :
Soit
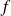une fonction continue par morceaux sur
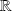, périodique de période
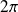et à valeurs dans
.
Les coefficients trigonométriques associés à
sont définis par :
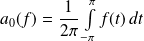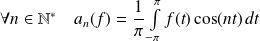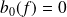et :
.
et :
.
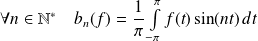La série de Fourier associée à
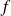est la série trigonométrique définie par :
.
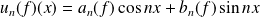Là aussi les intégrales peuvent être prises sur tout intervalle de longueur
.
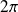Fondamental :
Propriétés
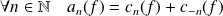et :
.
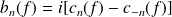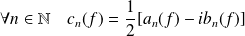et :
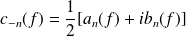
Si
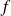est paire :
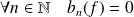et :
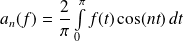. Si
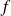est impaire :
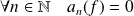et :
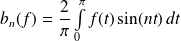. Si
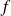est continue et de classe
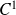par morceaux :
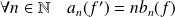et :
.
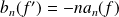Fondamental :
Inégalité de Bessel
Si
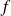est continue par morceaux sur
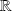et
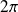-périodique :
.
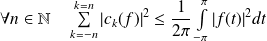Conséquences :
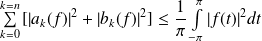.Les suites
,
,
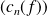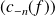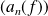et
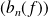convergent vers
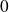.La suite
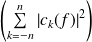et les séries
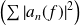et
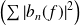convergent.Si
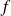est de classe
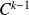sur
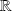et de classe
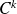par morceaux :
.
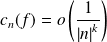