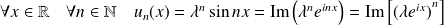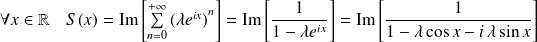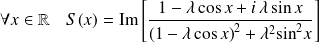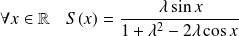Exo 9
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit un réel
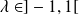et
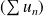la série de fonctions définie par :
.
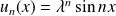Question
Montrer que la série
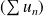est une série trigonométrique convergente sur
.
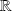Majorez
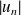pour montrer la convergence normale.
La série
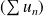est une série trigonométrique avec :
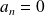et
.
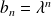De plus :
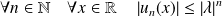, donc :
.
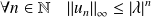Or
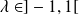, donc la série géométrique
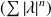est convergente.
Conclusion : La série trigonométrique
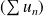converge normalement sur
.
Question
En déduire la valeur de l'intégrale :
.
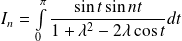Utilisez l'expression des coefficients trigonométriques de la fonction et leur unicité.
La somme
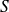de la série
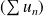est une fonction continue sur
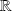car le dénominateur ne s'annule pas.
Donc :
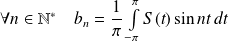, donc :
.
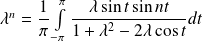Donc :
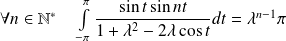si
.
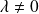Ce résultat reste vrai si
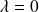et
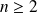car :
.
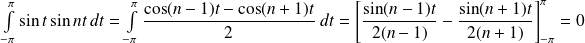Et pour
:
.
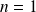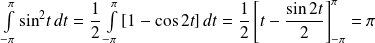Donc :
.
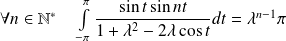Or la fonction
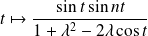est paire, donc :
.
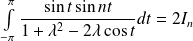Conclusion :
.
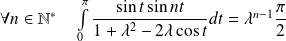