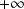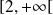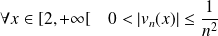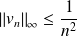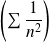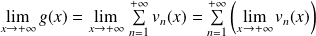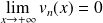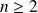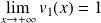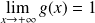Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
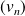la suite de fonctions définies sur
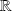par :
.
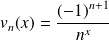Question
Déterminer l'ensemble de définition de la fonction
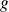définie par :
.
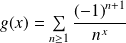Etudiez la convergence de la série.
La série
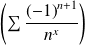diverge si
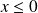car son terme général ne tend pas vers
.
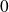Si
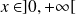, la suite
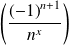décroît en valeur absolue vers
.
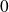Donc, d'après le critère des séries alternées, la série
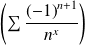est convergente.
Conclusion : L'ensemble de définition de la fonction
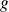est
.
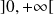Question
Question
Déterminer la limite de
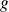en
.
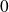Démontrez que :
.
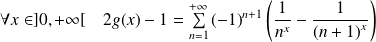Utilisez les propriétés des séries alternées pour encadrer
.
.
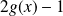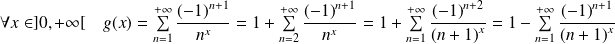Donc :
.
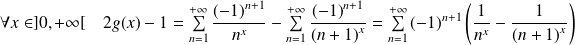Donc :
.
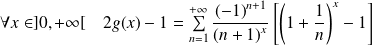Il s'agit d'une série alternée dont le terme général décroît en valeur absolue vers
.
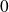Donc, si
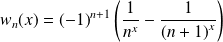, la série
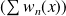est convergente.
Donc, d'après le critère des séries alternées, le reste
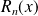d'ordre
est du signe de
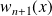et :
.
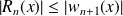En particulier :
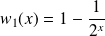, donc :
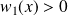, donc :
.
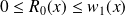Or :
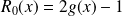. Donc :
.
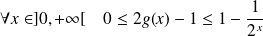Or :
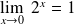. Donc :
.
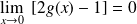Conclusion :
.
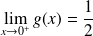Question
Démontrer que la fonction
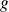est de classe
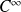sur son ensemble de définition et calculer ses dérivées successives.
Démontrez que toutes les séries
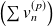convergent uniformément sur tout segment de
.
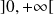Les fonctions
:
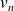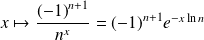sont de classe
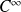sur
.
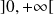Les dérivées successives sont :
.
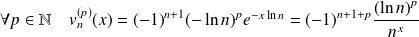Pour tout entier
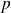, les séries
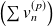sont donc des séries alternées.
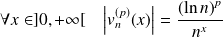. Donc :
.
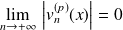Soit
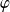la fonction définie par :
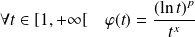(avec
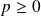et
).
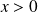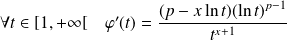est négatif si
.
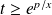Donc la suite
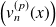décroît en valeur absolue vers
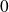si
.
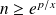Soit
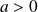et
:
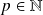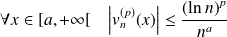. Et :
.
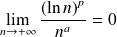Donc, pour tout entier
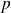, la suite
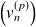converge uniformément vers
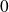sur
.
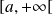Donc, d'après le critère des séries alternées, la série
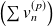converge uniformément sur
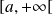pour tout entier
.
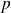Donc toutes les séries
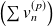convergent uniformément sur tout segment de
.
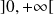Conclusion : La fonction
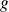est de classe
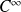sur
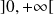et
.
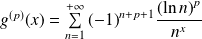Question
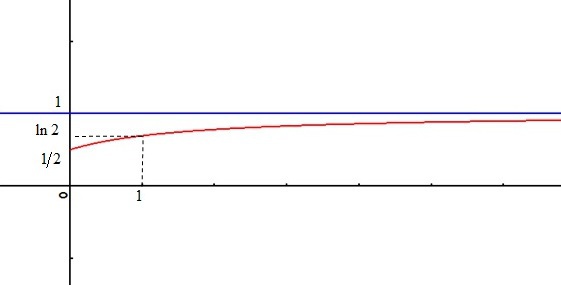
En déduire l'allure de la courbe représentative de
.
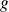Dressez le tableau de variations de la fonction.
En particulier :
.
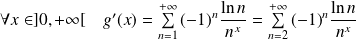Il s'agit d'une série alternée dont le terme général décroît en valeur absolue vers
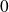, donc d'après le critère des séries alternées,
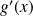est du signe du premier terme.
Donc :
.
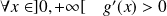On obtient le tableau de variations suivant :
.
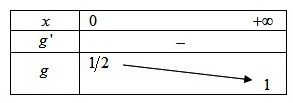
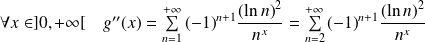Il s'agit d'une série alternée dont le terme général décroît en valeur absolue vers
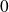, donc d'après le critère des séries alternées,
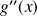est du signe du premier terme.
Donc :
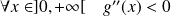. Donc la fonction
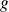est concave.
De plus :
.
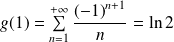Question
Démontrer que :
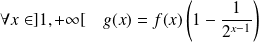où
.
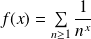Démontrez que la convergence des deux séries est uniforme sur tout segment de
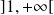, puis séparez les termes de rangs pairs et impairs.
Sur
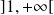, les deux séries
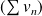et
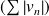sont convergentes. Soit
.
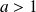La fonction
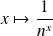décroît sur
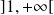. Donc :
.
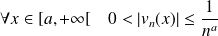Donc, sur
:
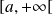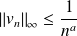. Or la série de Riemann
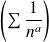converge.
Donc la convergence des deux séries est normale sur
.
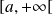Donc la convergence des deux séries est uniforme sur tout segment de
.
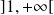On peut donc changer l'ordre des termes des deux séries sur
.
.
.
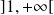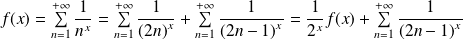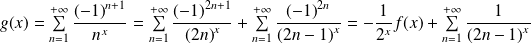Conclusion :
.
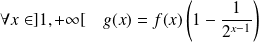