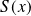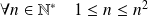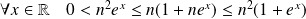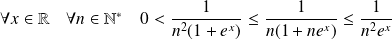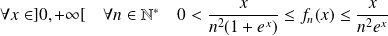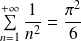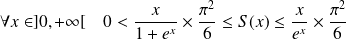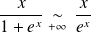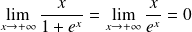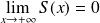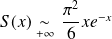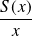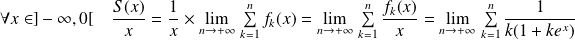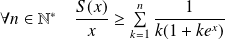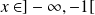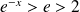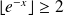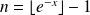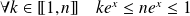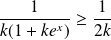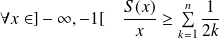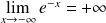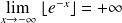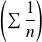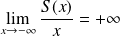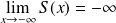Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
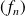la suite de fonctions définies par :
.
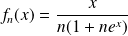Question
Démontrer que la série
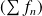converge simplement sur
.
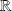Déterminez un équivalent de
.
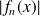Si
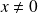, alors :
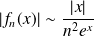et
.
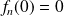Donc, si
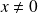, la série
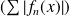est de même nature que la série
.
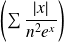Or la série
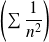est convergente. Donc la série
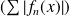est convergente.
Donc pour tout réel
, la série
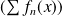est absolument convergente, donc convergente.
Conclusion : La série
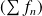converge simplement sur
.
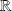Question
Démontrer que la somme
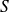de la série
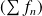est de classe
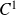sur
.
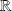Démontrez que la série
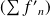converge normalement sur
.
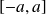Les fonctions
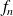sont de classe
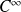sur
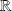et :
.
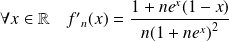Donc :
.
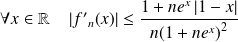Soit
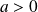. Alors :
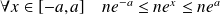, et :
.
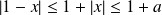Donc :
.
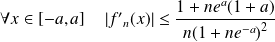Or :
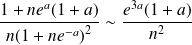, donc la série
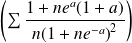converge.
Donc la série
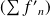converge normalement sur
.
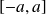Donc la série
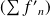converge uniformément sur tout segment de
.
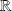Conclusion : La somme
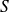de la série
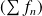est de classe
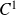sur
.
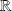Question
Etudier le sens de variations de la fonction
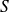sur
.
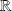Etudiez le signe de la dérivée dans les cas
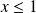et
.
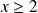Sur
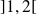, étudiez le sens de variations des fonctions
.
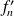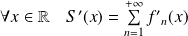, et :
.
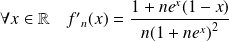Pour tout réel
,
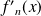est du signe de
.
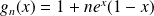Si
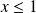, alors :
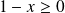, donc :
.
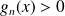Si
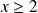, alors :
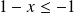et :
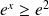, donc :
.
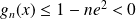Donc :
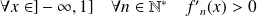, donc :
.
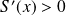Et :
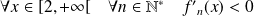, donc :
.
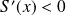Il reste à faire l'étude entre
et
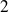. On étudie les variations des fonctions
.
.
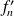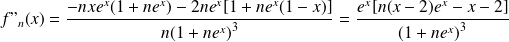Donc :
.
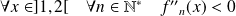Donc les fonctions
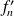sont toutes strictement décroissantes entre
et
.
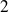Donc la fonction
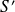est strictement décroissante entre
et
.
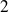Or elle est continue avec
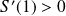et
.
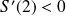Donc l'équation
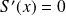admet une unique solution
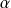entre
et
.
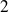La fonction
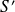est donc positive sur
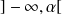et négative sur
.
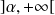Conclusion : La fonction
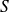est croissante sur
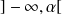et décroissante sur
.
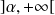Question
Question
Question
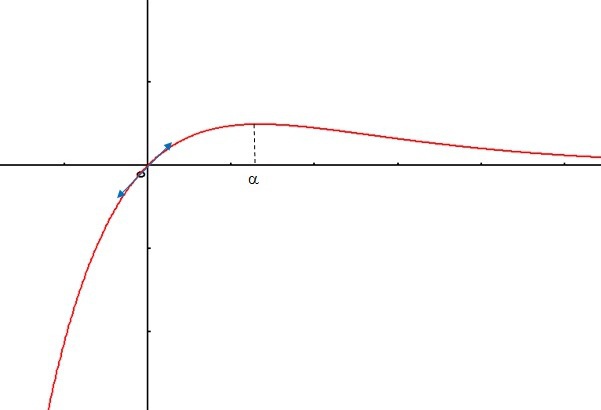
En déduire l'allure de la courbe représentative de
.
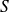On obtient le tableau de variations suivant :
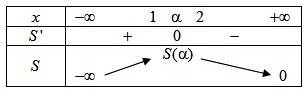
En
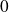, on a :
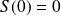et :
.
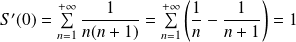En
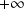, la courbe admet une asymptote horizontale.
En
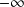, la courbe admet une branche parabolique de direction
.
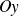