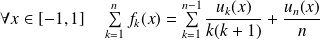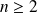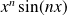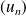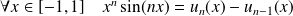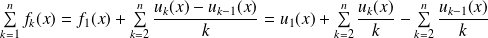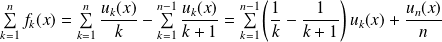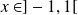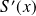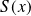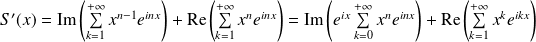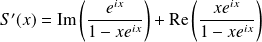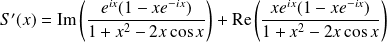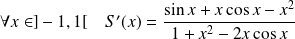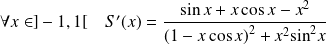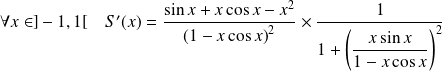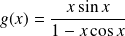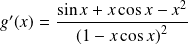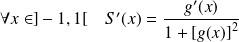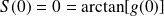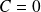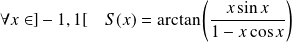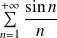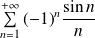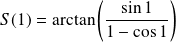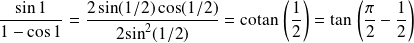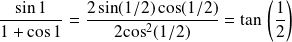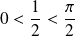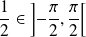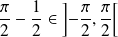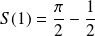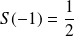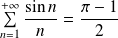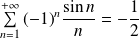Exo 14
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
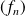 la suite de fonctions définies par :
la suite de fonctions définies par :
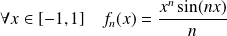 .
.
Soit
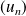 la suite de fonctions définies par :
la suite de fonctions définies par :
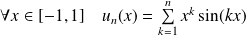 .
.
Question
Montrer que la suite
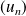 est bornée.
est bornée.
Utilisez les nombres complexes pour calculer
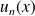 .
.
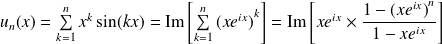 car
car
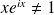 .
.
Donc :
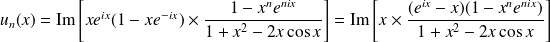 .
.
Donc :
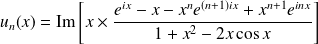 .
.
Donc :
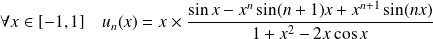 .
.
Donc :
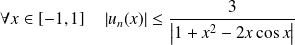 .
.
Or :
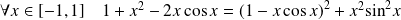 .
.
Donc la fonction
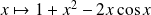 est une fonction positive, continue sur
est une fonction positive, continue sur
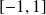 et qui ne s'annule pas sur
et qui ne s'annule pas sur
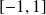 .
.
Elle admet donc un minimum
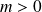 . Et :
. Et :
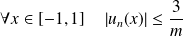 .
.
Conclusion : La suite de fonctions
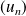 est bornée.
est bornée.
Question
Question
En déduire que la série
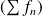 converge siumplement sur
converge siumplement sur
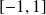 .
.
La suite
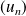 est bornée, donc :
est bornée, donc :
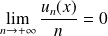 .
.
Et :
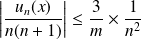 , donc la série
, donc la série
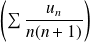 est normalement convergente.
est normalement convergente.
Donc, pour tout
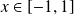 , la suite
, la suite
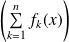 admet une limite finie.
admet une limite finie.
Conclusion : La série
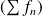 converge siumplement sur
converge siumplement sur
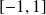 .
.
Remarque :
La convergence sur
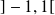 était plus facile car
était plus facile car
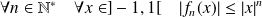 .
.
Le problème était en
 et en
et en
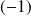 .
.
Question
Montrer que la somme
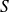 de la série
de la série
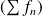 est continue sur
est continue sur
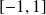 .
.
Etudiez la continuité de la somme de la série
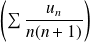 .
.
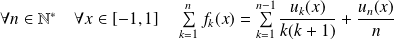 et
et
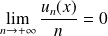 .
.
Donc :
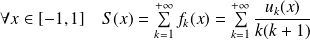 .
.
Or la série
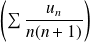 est normalement, donc uniformément convergente.
est normalement, donc uniformément convergente.
Et les fonctions
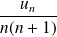 sont continues sur
sont continues sur
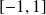 .
.
Donc la somme de la série
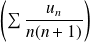 est continue sur
est continue sur
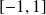 .
.
Conclusion : La somme
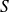 de la série
de la série
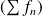 est continue sur
est continue sur
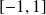 .
.
Question
Montrer que la somme
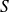 de la série
de la série
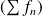 est de classe
est de classe
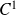 sur
sur
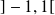 .
.
Utilisez le théorème de dérivation.
Les fonctions
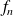 sont de classe
sont de classe
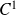 sur
sur
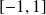 .
.
Et :
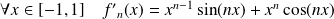 , donc :
, donc :
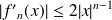 .
.
Donc, pour tout segment
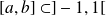 :
:
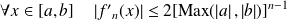 .
.
Donc la série
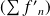 est normalement convergente, donc uniformément convergente sur tout segment contenu dans
est normalement convergente, donc uniformément convergente sur tout segment contenu dans
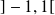 .
.
Conclusion : La somme
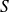 de la série est de classe
de la série est de classe
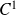 sur
sur
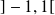 et
et
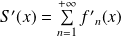 .
.