Exo 8
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
Démontrer que :
.
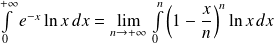Ramenez vous à deux intégrales sur
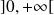, puis utilisez le théorème de convergence dominée.
La fonction
:
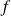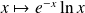est continue sur
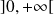. De plus :
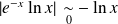et
.
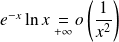Donc l'intégrale
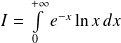est convergente.
Pour tout
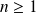, on pose :
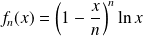si
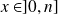et
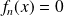sinon.
La fonction
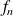est continue par morceaux sur
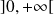et
.
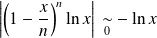Donc l'intégrale
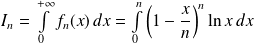est convergente.
Pour tout
:
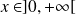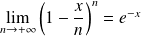. Donc :
.
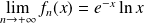Donc la suite
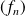converge simplement vers la fonction
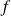sur
.
.
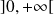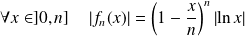Or, par concavité :
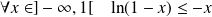. Donc :
.
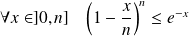Et :
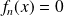sur
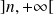. Donc :
.
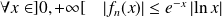Or la fonction
:
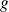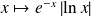est intégrable sur
.
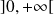Donc, d'après le théorème de convergence dominée :
.
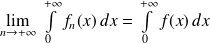Conclusion :
.
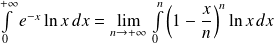Question
En déduire le calcul de
.
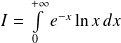Effectuez un changement de variable, puis une intégration par parties pour calculer
.
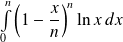Calculons
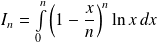par changement de variable :
.
.
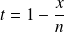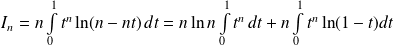On intègre par parties la deuxième intégrale.
.
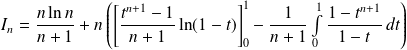Donc :
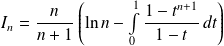. Or :
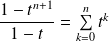si
.
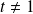Donc :
.
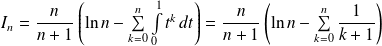On reconnaît la série harmonique :
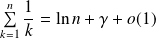où
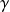est la constante d'Euler.
Donc :
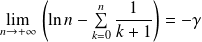. Donc :
.
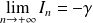Conclusion :
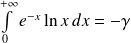où
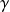est la constante d'Euler.
