Propriétés de la convergence uniforme
Les fonctions considérées sont définies sur un intervalle
 de
de
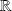 à valeurs réelles ou complexes.
à valeurs réelles ou complexes.
Fondamental :
Opérations algébriques
Soit
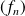 et
et
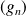 deux suites de fonctions qui convergent uniformément sur
deux suites de fonctions qui convergent uniformément sur
 vers des fonctions
vers des fonctions
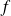 et
et
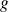 .
.
La suite de fonctions
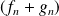 converge uniformément sur
converge uniformément sur
 vers
vers
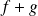 .
.Si
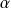 est un complexe, la suite de fonctions
est un complexe, la suite de fonctions
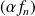 converge uniformément sur
converge uniformément sur
 vers
vers
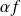 .
.Si les fonctions
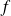 et
et
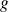 sont bornées sur
sont bornées sur
 , la suite
, la suite
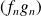 converge uniformément sur
converge uniformément sur
 vers
vers
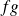 .
.
Fondamental :
Composition
Si
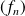 est une suite de fonctions qui converge uniformément sur
est une suite de fonctions qui converge uniformément sur
 vers une fonction
vers une fonction
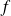 et si
et si
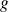 est une fonction définie sur un intervalle
est une fonction définie sur un intervalle
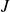 de
de
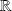 à valeurs dans
à valeurs dans
 , alors la suite de fonctions
, alors la suite de fonctions
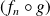 converge uniformément sur
converge uniformément sur
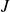 vers la fonction
vers la fonction
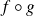 .
.Si
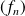 est une suite de fonctions à valeurs réelles qui converge uniformément sur
est une suite de fonctions à valeurs réelles qui converge uniformément sur
 vers une fonction
vers une fonction
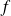 et si
et si
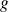 est une fonction uniformément continue sur
est une fonction uniformément continue sur
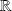 , alors la suite de fonctions
, alors la suite de fonctions
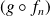 converge uniformément sur
converge uniformément sur
 vers la fonction
vers la fonction
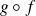 .
.
Fondamental :
Bornes
Soit
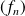 une suite de fonctions définies sur
une suite de fonctions définies sur
 à valeurs réelles ou complexes qui converge uniformément sur
à valeurs réelles ou complexes qui converge uniformément sur
 vers une fonction
vers une fonction
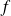 .
.
Si
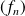 est une suite de fonctions bornées, alors la fonction
est une suite de fonctions bornées, alors la fonction
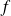 est bornée.
est bornée.
Fondamental :
Limite
Soit
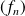 une suite de fonctions définies sur
une suite de fonctions définies sur
 à valeurs réelles ou complexes qui converge uniformément sur
à valeurs réelles ou complexes qui converge uniformément sur
 vers une fonction
vers une fonction
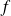 .
.
Si les fonctions
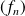 admettent en
admettent en
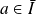 une limite finie
une limite finie
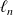 , alors la suite
, alors la suite
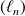 est convergente et la fonction
est convergente et la fonction
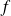 admet en
admet en
 la limite :
la limite :
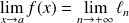 .
.
Donc, sous ces hypothèses, on peut intervertir les limites :
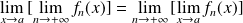 .
.
Fondamental :
Continuité
Soit
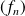 une suite de fonctions définies sur
une suite de fonctions définies sur
 à valeurs réelles ou complexes qui converge uniformément sur
à valeurs réelles ou complexes qui converge uniformément sur
 vers une fonction
vers une fonction
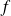 .
.
Si
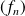 est une suite de fonctions continues sur
est une suite de fonctions continues sur
 , alors la fonction
, alors la fonction
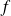 est continue sur
est continue sur
 .
.
Le théorème reste vrai même avec une convergence uniforme locale.
Fondamental :
Intégration
Soit
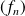 une suite de fonctions définies sur
une suite de fonctions définies sur
 à valeurs réelles ou complexes qui converge uniformément sur
à valeurs réelles ou complexes qui converge uniformément sur
 vers une fonction
vers une fonction
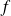 .
.
Si
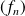 est une suite de fonctions continues sur
est une suite de fonctions continues sur
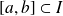 , alors la fonction
, alors la fonction
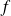 est continue sur
est continue sur
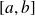 et :
et :
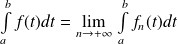 .
.
Donc, sous ces hypothèses, on peut intervertir la limite et l'intégrale :
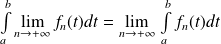 .
.
Pour les intégrales impropres, il faut en plus une hypothèse de domination.
Fondamental :
Théorème de convergence dominée :
Soit
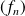 une suite de fonctions continues par morceaux sur
une suite de fonctions continues par morceaux sur
 à valeurs réelles ou complexes qui converge simplement sur
à valeurs réelles ou complexes qui converge simplement sur
 vers une fonction
vers une fonction
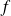 continue par morceaux sur
continue par morceaux sur
 .
.
S'il existe une fonction
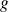 continue par morceaux et intégrable sur
continue par morceaux et intégrable sur
 telle que
telle que
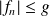 pour tout
pour tout
 , alors les fonctions
, alors les fonctions
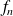 et
et
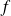 sont intégrables sur
sont intégrables sur
 et :
et :
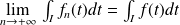 .
.
L'hypothèse de domination est indispensable.
Par exemple, la suite de fonctions
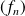 définie sur
définie sur
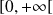 par :
par :
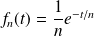 converge vers la fonction nulle (même uniformément !).
converge vers la fonction nulle (même uniformément !).
Et pourtant :
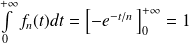 ne tend pas vers
ne tend pas vers
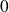 .
.
Fondamental :
Dérivation
Soit
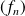 une suite de fonctions de classe
une suite de fonctions de classe
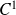 sur
sur
 à valeurs réelles ou complexes qui converge simplement sur
à valeurs réelles ou complexes qui converge simplement sur
 vers une fonction
vers une fonction
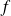 .
.
Si la suite
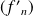 converge uniformément sur tout segment
converge uniformément sur tout segment
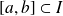 , alors :
, alors :
la suite
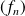 converge uniformément vers
converge uniformément vers
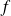 sur tout segment
sur tout segment
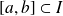 ,
,la fonction
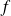 est de classe
est de classe
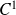 sur
sur
 ,
,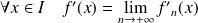 .
.
On en déduit un théorème pour les dérivées d'ordres supérieurs.
Fondamental :
Soit
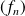 une suite de fonctions de classe
une suite de fonctions de classe
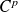 sur
sur
 à valeurs réelles ou complexes qui converge simplement sur
à valeurs réelles ou complexes qui converge simplement sur
 vers une fonction
vers une fonction
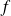 .
.
Si les suites
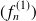 , ...,
, ...,
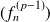 convergent simplement sur
convergent simplement sur
 et si la suite
et si la suite
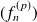 converge uniformément sur tout segment
converge uniformément sur tout segment
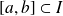 , alors :
, alors :
la suite
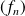 converge uniformément vers
converge uniformément vers
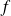 sur tout segment
sur tout segment
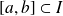 ,
,la fonction
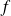 est de classe
est de classe
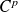 sur
sur
 ,
,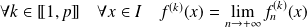 .
.





