Exo 16
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soit
 une partie non vide d'un espace vectoriel normé.
une partie non vide d'un espace vectoriel normé.
Question
Montrer que
 est fermée si et seulement si
est fermée si et seulement si
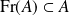 .
.
Une partie
 est fermée si et seulement si :
est fermée si et seulement si :
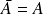 .
.
Si
 est fermée, alors :
est fermée, alors :
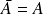 . Donc :
. Donc :
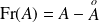 . Donc :
. Donc :
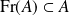 .
.
Réciproquement, supposons que :
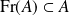 .
.
Pour toute partie
 non vide :
non vide :
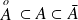 . Donc :
. Donc :
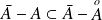 .
.
Donc :
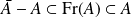 . Or :
. Or :
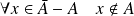 .
.
Donc :
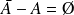 . Donc :
. Donc :
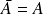 . Donc
. Donc
 est un fermé.
est un fermé.
Conclusion : Une partie
 non vide est fermée si et seulement si
non vide est fermée si et seulement si
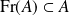 .
.
Question
Montrer que
 est ouverte si et seulement si
est ouverte si et seulement si
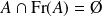 .
.
Une partie
 est ouverte si et seulement si :
est ouverte si et seulement si :
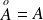 .
.
Si
 est ouverte, alors :
est ouverte, alors :
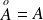 . Donc :
. Donc :
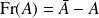 . Donc :
. Donc :
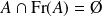 .
.
Réciproquement, supposons que :
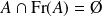 .
.
Pour toute partie
 non vide :
non vide :
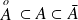 . Donc :
. Donc :
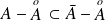 .
.
Donc :
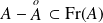 . Or :
. Or :
 . Donc :
. Donc :
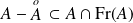 .
.
Donc :
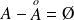 . Donc :
. Donc :
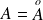 . Donc
. Donc
 est un ouvert.
est un ouvert.
Conclusion : Une partie
 non vide est ouverte si et seulement si
non vide est ouverte si et seulement si
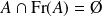 .
.
Question
Montrer que :
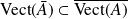 .
.
Tout élément de
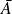 est limite d'une suite d'éléments de
est limite d'une suite d'éléments de
 .
.
Soit
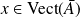 . Donc
. Donc
 est combinaison linéaire d'éléments de
est combinaison linéaire d'éléments de
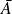 .
.
Il existe
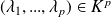 et
et
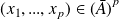 tels que :
tels que :
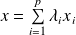 .
.
Or tout élément de
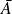 est limite d'une suite d'éléments de
est limite d'une suite d'éléments de
 .
.
Donc pour tout
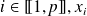 est limite d'une suite
est limite d'une suite
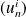 d'éléments de
d'éléments de
 .
.
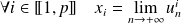 , donc :
, donc :
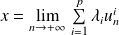 .
.
La suite de terme général
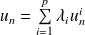 est une suite d'éléments de
est une suite d'éléments de
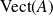 .
.
Donc :
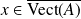 .
.
Conclusion :
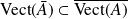 .
.
Question
Montrer que, si
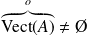 , alors :
, alors :
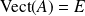 .
.
Raisonnez par l'absurde.
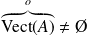 , donc il existe
, donc il existe
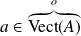 et
et
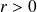 tel que :
tel que :
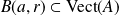 .
.
On raisonne par l'absurde : on suppose que
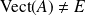 .
.
Soit
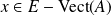 . Donc
. Donc
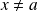 , et donc :
, et donc :
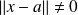 .
.
Le vecteur
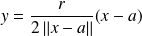 vérifie :
vérifie :
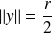 , donc :
, donc :
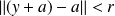 .
.
Donc :
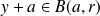 , donc :
, donc :
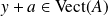 .
.
Or
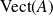 est un sous-espace vectoriel de
est un sous-espace vectoriel de
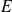 et
et
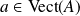 .
.
Donc :
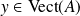 , donc :
, donc :
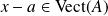 , et donc :
, et donc :
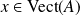 .
.
On aboutit donc à une contradiction car
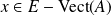 .
.
Conclusion : Si
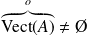 , alors :
, alors :
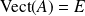 .
.
Question
Si
 est un sous espace vectoriel de
est un sous espace vectoriel de
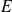 , l'adhérence et l'intérieur de
, l'adhérence et l'intérieur de
 sont-ils des sous-espaces vectoriels de
sont-ils des sous-espaces vectoriels de
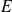 ?
?
Supposons que
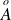 soit un sous espace vectoriel de
soit un sous espace vectoriel de
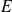 , donc :
, donc :
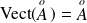 .
.
Donc :
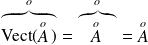 car
car
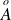 est ouvert.
est ouvert.
Donc :
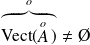 , et donc d'après la question précédente :
, et donc d'après la question précédente :
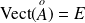 .
.
Donc, si
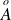 est un sous espace vectoriel, alors :
est un sous espace vectoriel, alors :
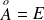 . Or :
. Or :
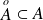 . Donc :
. Donc :
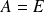 .
.
Réciproquement, si
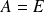 , alors
, alors
 est un ouvert, donc
est un ouvert, donc
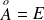 , donc
, donc
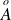 est un sous espace vectoriel de
est un sous espace vectoriel de
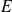 .
.
Conclusion : L'intérieur d'un sous-espace vectoriel
 de
de
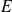 est un sous-espace vectoriel de
est un sous-espace vectoriel de
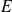 si et seulement si
si et seulement si
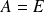 .
.
Remarque :
Conséquence : Le seul sous-espace vectoriel ouvert de
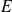 est
est
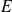 .
.
Si
 est un sous-espace vectoriel de
est un sous-espace vectoriel de
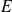 , alors :
, alors :
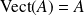 .
.
Donc, d'après la troisième question :
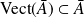 . Or :
. Or :
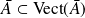 .
.
Donc :
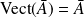 . Donc
. Donc
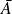 est un sous-espace vectoriel.
est un sous-espace vectoriel.
Conclusion : L'adhérence d'un sous-espace vectoriel
 de
de
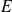 est toujours un sous-espace vectoriel de
est toujours un sous-espace vectoriel de
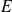 .
.
Remarque :
Remarque : Dans un espace vectoriel de dimension finie sur
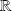 ou
ou
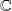 , tout sous-espace vectoriel est fermé.
, tout sous-espace vectoriel est fermé.
En effet,
 est un sous-espace vectoriel, donc il admet une base
est un sous-espace vectoriel, donc il admet une base
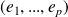 .
.
Soit
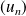 une suite convergente d'éléments de
une suite convergente d'éléments de
 :
:
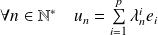 .
.
La suite
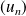 est convergente, donc c'est une suite de Cauchy.
est convergente, donc c'est une suite de Cauchy.
Donc :
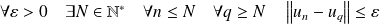 .
.
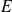 est de dimension finie, donc on peut choisir n'importe quelle norme.
est de dimension finie, donc on peut choisir n'importe quelle norme.
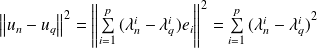 .
.
Donc :
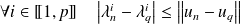 .
.
Donc pour tout
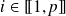 , la suite
, la suite
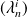 est une suite de Cauchy de
est une suite de Cauchy de
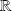 ou
ou
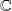 .
.
Donc elle converge. Soit
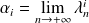 .
.
Donc la suite
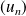 converge vers
converge vers
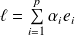 qui appartient à
qui appartient à
 .
.
Donc toute suite convergente d'éléments de
 a sa limite dans
a sa limite dans
 , donc
, donc
 est fermé.
est fermé.





