Topologie
Dans ce qui suit,
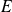désigne un espace vectoriel normé sur
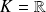ou
.
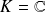Définition :
Une partie
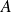de
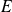est un ouvert si :
.
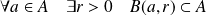Exemples :
,
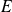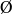et les boules ouvertes sont des ouverts.
Dans
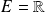, les intervalles ouverts sont des ouverts.
Fondamental :
Propriétés :
Une réunion d'un nombre fini ou infini d'ouverts est un ouvert.
Une intersection finie d'ouverts est un ouvert.
Une application
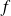de
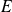dans
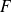est continue sur
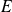si et seulement si l'image réciproque de tout ouvert de
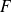est un ouvert de
.
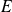Attention ! Une intersection infinie d'ouverts n'est pas toujours un ouvert. Par exemple :
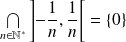n'est pas un ouvert.
Définition :
Une partie
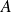de
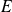est un fermé si son complémentaire
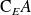dans
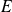est un ouvert.
Exemples :
,
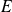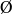et les boules fermées sont des fermés.
Dans
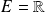, les intervalles fermés sont des fermés, ainsi que les intervalles de la forme
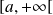ou
.
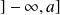Fondamental :
Propriétés :
Une réunion finie de fermés est un fermé.
Une intersection d'un nombre fini ou infini de fermés est un fermé.
Une partie
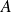de
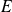est un fermé si et seulement si toute suite convergente d'éléments de
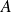a sa limite dans
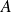.Une application
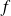de
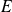dans
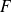est continue sur
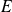si et seulement si l'image réciproque de tout fermé de
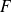est un fermé de
.
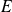Définition :
Un élément
de
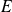est adhérent à une partie
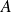non vide de
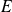si :
.
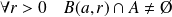L'adhérence d'une partie
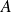non vide de
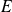est l'ensemble
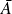des points adhérents à
.
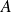Un point
est adhérent à une partie
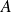si et seulement si il existe une suite d'éléments de
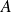qui converge vers
.
Un point
est valeur d'adhérence d'une suite s'il existe une suite extraite qui converge vers
.
Fondamental :
Propriétés :
.
.
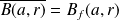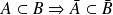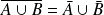mais :
.-
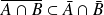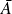est le plus petit fermé contenant
.
-
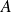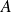est un fermé si et seulement si :
. -
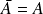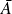est l'intersection de tous les fermés contenant
.
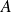Définition :
Une partie
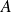de
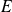est dense dans
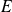si :
.
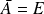Par exemple, l'ensemble des rationnels et l'ensemble des irrationnels sont denses dans l'ensemble des réels.
Définition :
Un élément
de
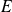est intérieur à une partie
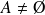si :
.
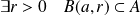L'intérieur
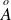d'une partie
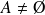est l'ensemble des points intérieurs à
.
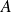Fondamental :
Propriétés :
.-
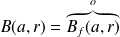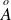est le plus grand ouvert contenu dans
.
-
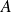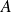est un ouvert si et seulement si :
. -
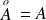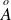est la réunion de tous les ouverts contenus dans
.
.
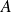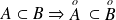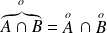, mais :
.
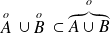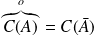et :
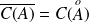. (complémentaires).
Définition :
La frontière d'une partie
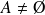est :
.
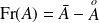Fondamental :
Propriétés :
Si
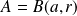, alors :
.
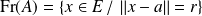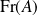est un fermé et :
.
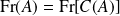