Exo 15
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Soient
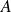et
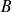deux parties non vides d'un espace vectoriel normé
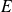et
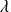un réel non nul.
On note :
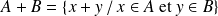et :
.
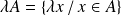Question
Montrer que si
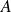et
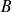sont des ouverts, alors
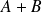et
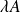sont des ouverts.
Utilisez la définition des ouverts.
On suppose que
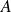et
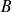sont des ouverts de
.
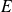Soit
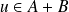. Donc il existe
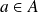et
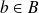tels que
.
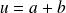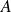est un ouvert, donc il existe
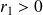tel que :
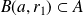. De même, il existe
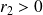tel que :
.
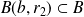Pour tout
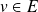, on peut remarquer que :
.
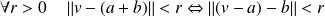Soit
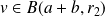. Donc :
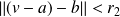, donc :
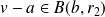, donc :
.
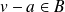Or :
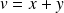avec
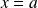et
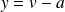, donc :
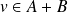. Donc :
.
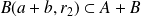Donc, pour tout
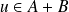, il existe une boule de centre
incluse dans
.
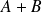Conclusion : Si
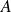et
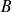sont des ouverts, alors
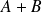est un ouvert.
Soit
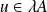. Donc il existe
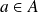tel que
.
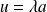Pour tout
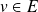, on peut remarquer que :
.
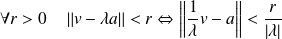Soit
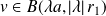. Donc :
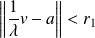, donc :
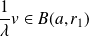, donc :
.
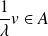Or :
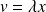avec :
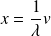. Donc :
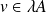. Donc :
.
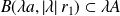Donc, pour tout
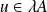, il existe une boule de centre
incluse dans
.
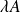Conclusion : Si
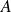est un ouvert, alors
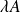est un ouvert.
Question
Montrer que si
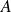et
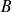sont des fermés, alors
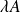est un fermé, mais pas forcément
.
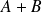Raisonnez sur les complémentaires qui sont ouverts.
On suppose que
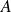est un fermé de
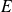, donc son complémentaire
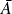est un ouvert.
Or :
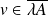si et seulement si :
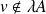, donc si :
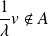, donc si :
.
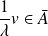Donc :
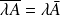qui est un ouvert d'après la question précédente car
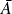est un ouvert.
Conclusion : Si
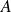est un fermé, alors
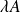est un fermé.
On suppose que
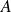et
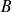sont des fermés de
.
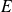Pour montrer que
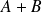n'est pas toujours un fermé, on donne un contre-exemple.
On considère l'espace vectoriel
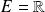muni de la valeur absolue.
Une réunion même infinie de fermés de
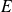est un fermé de
.
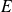Donc :
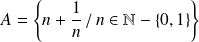et :
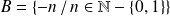sont des fermés de
.
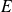Leur somme est :
.
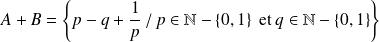Or :
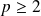, donc
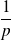n'est pas un entier, donc :
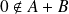. Donc
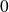appartient au complémentaire de
.
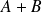Si
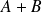était fermé, son complémentaire serait ouvert, et il existerait une boule
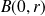qui ne contiendrait aucun élément de
.
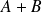Or :
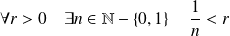, donc :
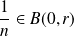. Et :
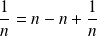, donc :
.
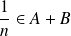Donc toute boule de centre
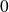contient au moins un élément de
.
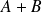Donc le complémentaire de
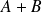n'est pas ouvert, donc
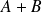n'est pas fermé.
Conclusion : La somme de deux fermés n'est pas toujours un fermé.
