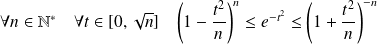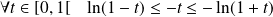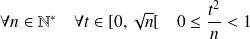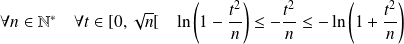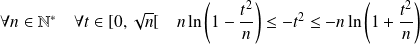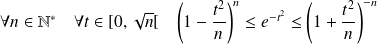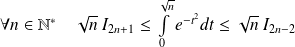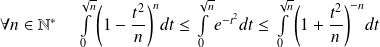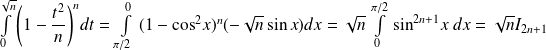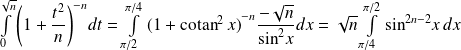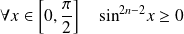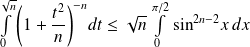Intégration sur un intervalle quelconque

Exo 4

Commencez par chercher à résoudre l'exercice par vous-même.

Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.

Une solution détaillée vous est ensuite proposée.

Question

Etudier la convergence de l'intégrale de Gauss : .

Indice

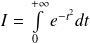Majorez la fonction à intégrer.

Solution

La fonction : 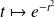est continue sur 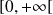et positive.

Donc l'intégrale est impropre seulement en .

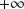L'intégrale 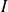est de même nature que l'intégrale : .

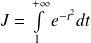Or : 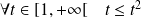, donc : .

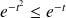Or l'intégrale 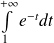est convergente : .

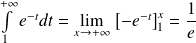Donc, par majoration, l'intégrale 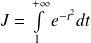est convergente.

Conclusion : L'intégrale de Gauss 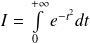est convergente.

Question

Démontrer que : .

Indice

Utilisez la fonction logarithme.

Solution

La fonction logarithme est concave : .

Donc : et : .

Donc : .

Or : .

Donc : .

Donc : .

Donc : .

Et par continuité, l'inégalité reste vraie pour .

Conclusion : .

Question

En déduire que : en posant .

Indice

Utilisez la question précédente pour encadrer l'intégrale et effectuez des changements de variable.

Solution

.

Donc : .

Dans la première intégrale, on pose : , donc : et .

Donc : .

Dans la deuxième intégrale, on pose , donc : et : .

Donc : .

Or : . Donc : .

Conclusion : .

Question

En déduire le calcul de l'intégrale de Gauss : .

Indice

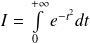Utilisez les propriétés des intégrales de Wallis.

Solution

Les intégrales 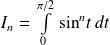sont les intégrales de Wallis, déjà étudiées dans un exercice.

On a démontré que : 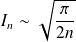. Donc : 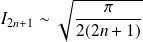et : .

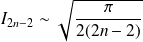Donc : 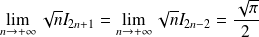. Donc : .

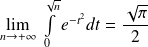Conclusion : L'intégrale de Gauss 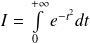est égale à .

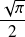PrécédentPrécédentSuivantSuivant
AccueilAccueilImprimerImprimer Paternité - Pas d'Utilisation Commerciale - Partage des Conditions Initiales à l'IdentiqueRéalisé avec Scenari (nouvelle fenêtre)