Convergence d'intégrales de fonctions positives
Les fonctions considérées sont définies sur un intervalle
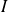de
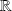à valeurs réelles et positives.
Fondamental :
Soit
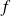une fonction continue par morceaux sur un intervalle
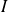à valeurs réelles positives.
Alors
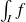converge si et seulement si il existe un réel
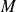tel que :
.
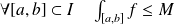Alors
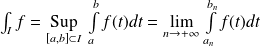où
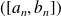est une suite telle que :
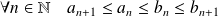et
.
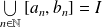Fondamental :
Relation d'ordre
Si
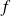et
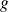sont continues par morceaux sur
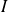telles que
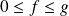, alors :
Si
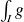converge, alors
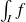converge et
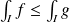.Si
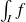diverge, alors
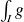diverge.
Fondamental :
Comparaison locale
Soient
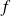et
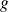deux fonctions continues par morceaux à valeurs réelles positives sur
.
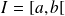Si
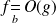et si
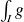converge, alors
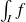converge.Si
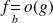et si
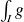converge, alors
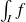converge.Si
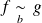, alors les intégrales
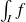et
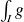sont de même nature.
On a évidemment des résultats analogues par comparaison en
si
.
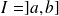On compare donc les intégrales à étudier avec quelques intégrales usuelles.
Fondamental :
Intégrales de Riemann (
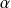est réel) : 
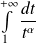converge si et seulement si
.
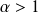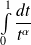converge si et seulement si
.
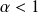Intégrales de Bertrand (
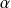et
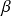sont réels) : 
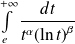converge si et seulement si
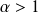ou
.
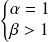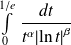converge si et seulement si
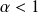ou
.
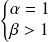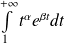converge si et seulement si
.
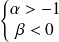On peut en déduire par exemple que
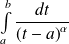et
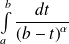convergent si et seulement si
.
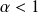