Intégrales de Wallis
Définition :
Les intégrales
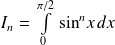et
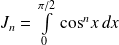sont appelées intégrales de Wallis.
Fondamental :
Propriété :
.
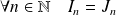On effectue dans
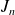le changement de variable
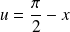. Donc :
.
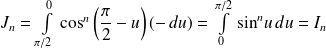Fondamental :
Propriété : La suite
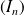est décroissante et convergente.
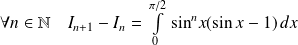. Or :
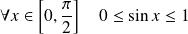, donc :
.
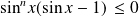Et
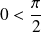, donc :
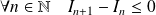. Donc la suite
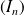est décroissante.
Elle est minorée p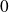ar
car :
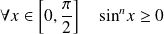. Donc la suite
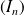est convergente.
Fondamental :
Propriétés :
.
.
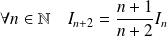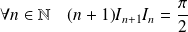On intègre
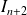par parties en posant :
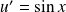et
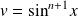. Donc :
.
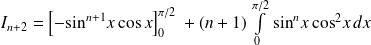Donc :
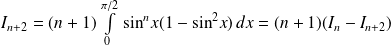. Donc :
.
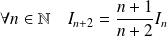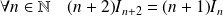, donc :
.
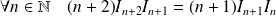Donc la suite de terme général
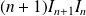est stationnaire (constante). Donc :
.
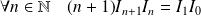Or :
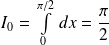et :
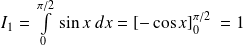. Donc :
.
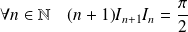Fondamental :
Propriété :
.
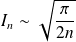La suite est décroissante, donc :
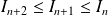, donc :
.
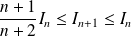L'intégrale
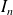n'est pas nulle car la fonction
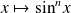garde un signe constant et n'est pas identiquement nulle sur l'intervalle
.
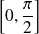Donc :
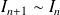. Or :
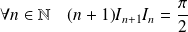, donc :
.
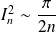Donc :
.
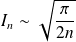