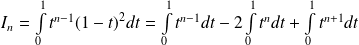Exo 13
Commencez par chercher à résoudre l'exercice par vous-même.
Si vous manquez d'idée pour débuter, consultez l'indice fourni et recommencez à chercher.
Une solution détaillée vous est ensuite proposée.
Question
En déduire que :
.
Indice
Démontrez que la série est convergente et exprimez ses sommes partielles à l'aide des intégrales précédentes.
Solution
Il s'agit de la somme de la série à termes positifs :
.
Or :
.
Donc la série
est de même nature que la série
, donc convergente.
La somme partielle d'ordre
est :
.
Donc :
.
Si
, alors :
.
Et si
, alors :
. Donc l'égalité est vraie aussi pour
.
Donc :
.
Or :
. Donc :
.
Donc :
.
Conclusion :
.
